��Ŀ����
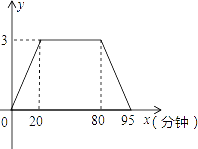
����Ŀ����ͼ��������![]() ��x�ύ��A��B���㣬��B��1��0��
��x�ύ��A��B���㣬��B��1��0��
��1���������ߵĽ���ʽ�͵�A�����ꣻ
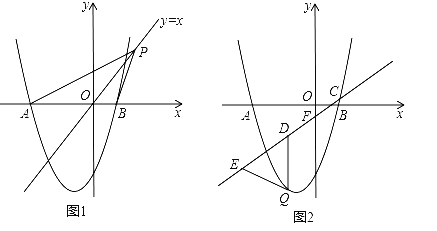
��2����ͼ1����P��ֱ��y=x�ϵĶ��㣬��ֱ��y=xƽ�֡�APBʱ�����P�����ꣻ
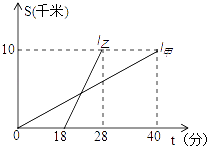
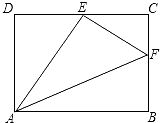
��3����ͼ2����ֱ֪��![]() �ֱ���x�ᡢy�ύ��C��F���㣬��Q��ֱ��CF�·����������ϵ�һ�����㣬����Q��y���ƽ���ߣ���ֱ��CF�ڵ�D����E���߶�CD���ӳ����ϣ�����QE���ʣ���QDΪ���ĵ�����QDE������Ƿ�������ֵ�������ڣ������������ֵ���������ڣ���˵�����ɣ�
�ֱ���x�ᡢy�ύ��C��F���㣬��Q��ֱ��CF�·����������ϵ�һ�����㣬����Q��y���ƽ���ߣ���ֱ��CF�ڵ�D����E���߶�CD���ӳ����ϣ�����QE���ʣ���QDΪ���ĵ�����QDE������Ƿ�������ֵ�������ڣ������������ֵ���������ڣ���˵�����ɣ�
���𰸡���1��![]() ��A����3��0������2��P��
��A����3��0������2��P��![]() ��
��![]() ������3��QDΪ���ĵ��������ε�������ֵΪ
������3��QDΪ���ĵ��������ε�������ֵΪ![]() ��
��
��������
�����������1����B��������������߽���ʽ�����a��ֵ������������߽���ʽ������y=0���ɽ����Ӧ���̵ĸ��������A�����ꣻ
��2������P��x���Ϸ�ʱ������AP��y���ڵ�B�䣬��֤��OBP�ա�OB��P�������B�����꣬���ô���ϵ���������ֱ��AP�Ľ���ʽ������ֱ��y=x�������P�����ꣻ����P��x���·�ʱ��ͬ������á�BPO=��B��PO���֡�B��PO�ڡ�APO���ڲ�����֪��ʱû�����������ĵ�P��
��3����Q��QH��DE�ڵ�H����ֱ��CF�Ľ���ʽ����õ�C��F�����꣬������������tan��QDH���ɷֱ���DQ��ʾ��QH��DH�ij�����DQ=DE��DQ=QE����������ֱ���DQ�ij���ʾ����QDE��������������Q�����꣬���ö��κ��������ʿ���á�QDE����������ֵ��
�����������1����B��1��0������![]() ���ɵ�a+2��3=0�����a=1���������߽���ʽΪ
���ɵ�a+2��3=0�����a=1���������߽���ʽΪ![]() ����y=0���ɵ�
����y=0���ɵ�![]() �����x=1��x=��3����A������Ϊ����3��0����
�����x=1��x=��3����A����������3��0����
��2����y=xƽ�֡�APB�����APO=��BPO����ͼ1����P����x���Ϸ���PA��y�ύ�ڵ�B�䣬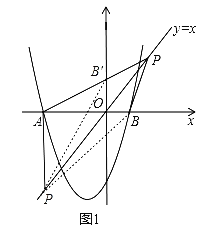
���ڵ�P��ֱ��y=x�ϣ���֪��POB=��POB��=45�㣬�ڡ�BPO�͡�B��PO��������POB=��POB����OP=OP����BOP=��B��OP�����BPO�ա�B��PO��ASA������BO=B��O=1����ֱ��AP����ʽΪy=kx+b����A��B�������������ɵ���![]() �������
�������![]() ����ֱ��AP����ʽΪ
����ֱ��AP����ʽΪ![]() ������
������ �������
�������![]() ����P��������
����P��������![]() ��
��![]() ����
����
��P����x���·�ʱ��ͬ���ɵá�BOP�ա�B��OP�����BPO=��B��PO���֡�B��PO�ڡ�APO���ڲ������APO�١�BPO������ʱû������������P�㣬���Ͽ�֪P������Ϊ��![]() ��
��![]() ����
����
��3����ͼ2����QH��CF����CF�ڵ�H����CFΪ![]() ��������C��
��������C��![]() ��0����F��0��
��0����F��0��![]() ������tan��OFC=
������tan��OFC=![]() =
=![]() ����DQ��y�ᣬ���QDH=��MFD=��OFC����tan��HDQ=
����DQ��y�ᣬ���QDH=��MFD=��OFC����tan��HDQ=![]() ��������DQ=t��DH=
��������DQ=t��DH=![]() t��HQ=
t��HQ=![]() t���ߡ�QDE����DQΪ���ĵ��������Σ�����DQ=DE����S��DEQ=
t���ߡ�QDE����DQΪ���ĵ��������Σ�����DQ=DE����S��DEQ=![]() DEHQ=
DEHQ=![]() ��
��![]() t��t=
t��t=![]() ����DQ=QE����S��DEQ=
����DQ=QE����S��DEQ=![]() DEHQ=
DEHQ=![]() ��2DHHQ=
��2DHHQ=![]() ��
��![]() t��
t��![]() t=
t=![]() ����
����![]() ��
��![]() ���൱DQ=QEʱ��DEQ�������DQ=DEʱ��
���൱DQ=QEʱ��DEQ�������DQ=DEʱ��
��Q��������x��![]() ������D��x��
������D��x��![]() ������Q����ֱ��CF���·�����DQ=t=
������Q����ֱ��CF���·�����DQ=t=![]() =
=![]() ����x=
����x=![]() ʱ��tmax=3���ࣨS��DEQ��max=
ʱ��tmax=3���ࣨS��DEQ��max=![]() =
=![]() ������QDΪ���ĵ��������ε�������ֵΪ
������QDΪ���ĵ��������ε�������ֵΪ![]() ��
��