题目内容
如图,AD⊥AB,BC⊥AB,且AD=2,BC=3,AB=12,P是线段AB上的一个动点,连接PD,PC
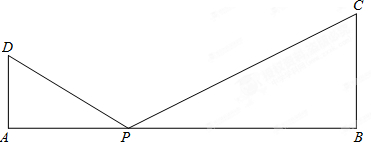
(1)设AP=x,用二次根式表示线段PD,PC的长;
(2)设y=PD+PC,求当点P在线段AB上运动时,y的最小值;
(3)利用(2)的结论,试求代数式
+
的最小值.

(1)设AP=x,用二次根式表示线段PD,PC的长;
(2)设y=PD+PC,求当点P在线段AB上运动时,y的最小值;
(3)利用(2)的结论,试求代数式
| x2+9 |
| (24-x)2+16 |
分析:(1)根据勾股定理即可用二次根式表示线段PD,PC的长;
(2)作D点关于AB的对称点D′,连接CD′,根据勾股定理求出CD′的长,即为y的最小值;
(3)根据勾股定理构造出图形,利用两点之间线段最短的方法即可求出代数式的最小值.
(2)作D点关于AB的对称点D′,连接CD′,根据勾股定理求出CD′的长,即为y的最小值;
(3)根据勾股定理构造出图形,利用两点之间线段最短的方法即可求出代数式的最小值.
解答:解:(1)在直角△ADP中,∵∠A=90°,AD=2,AP=x,
∴PD=
=
;
 在直角△BCP中,∵∠B=90°,AD=3,PB=AB-AP=12-x,
在直角△BCP中,∵∠B=90°,AD=3,PB=AB-AP=12-x,
∴PC=
=
;
(2)如右图.作D点关于AB的对称点D′,连接CD′,交AB于P,则PD′=PD,CD′=PD′+PC=PD+PC,即为y的最小值.
过D′作AB的平行线,交CB的延长线于E.
在△CED′中,∠E=90°,D′E=AB=12,CE=CB+BE=CB+AD=3+2=5,
由勾股定理,得CD′=
=13,
故y的最小值为13;
(3)如右图.构造图形,AB=24,AD⊥AB,AD=3,BC=4,PA=x,PB=24-x,
PD=
,PC=
,
由对称性可知,PC+PD的最小值为PC+PD′=CD′=
=
=25.
故代数式
+
的最小值为25.
∴PD=
| AD2+AP2 |
| 4+x2 |
 在直角△BCP中,∵∠B=90°,AD=3,PB=AB-AP=12-x,
在直角△BCP中,∵∠B=90°,AD=3,PB=AB-AP=12-x,∴PC=
| PB2+BC2 |
| (12-x)2+9 |
(2)如右图.作D点关于AB的对称点D′,连接CD′,交AB于P,则PD′=PD,CD′=PD′+PC=PD+PC,即为y的最小值.
过D′作AB的平行线,交CB的延长线于E.
在△CED′中,∠E=90°,D′E=AB=12,CE=CB+BE=CB+AD=3+2=5,
由勾股定理,得CD′=
| D′E2+CE2 |
故y的最小值为13;
(3)如右图.构造图形,AB=24,AD⊥AB,AD=3,BC=4,PA=x,PB=24-x,
PD=
| x2+9 |
| (24-x)2+16 |
由对称性可知,PC+PD的最小值为PC+PD′=CD′=
| D′E2+CE2 |
| 242+(4+3)2 |
故代数式
| x2+9 |
| (24-x)2+16 |
点评:本题考查了勾股定理,轴对称-最短路线问题,构造出图形利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目

 19、如图,AD⊥AB,BD⊥BC,AB=3,AD=4,CD=13,求BC的大小?
19、如图,AD⊥AB,BD⊥BC,AB=3,AD=4,CD=13,求BC的大小? 如图,AD•AB=AE•AC,若AD=3,AC=6,DE=4,则BC=
如图,AD•AB=AE•AC,若AD=3,AC=6,DE=4,则BC= 如图,AD⊥AB,AE⊥AC,AD=AB,AE=AC,则下列各式正确的是( )
如图,AD⊥AB,AE⊥AC,AD=AB,AE=AC,则下列各式正确的是( ) 如图,AD=AB,∠C=∠E,∠CDE=55°,则∠ABE=
如图,AD=AB,∠C=∠E,∠CDE=55°,则∠ABE=