题目内容
【题目】当x分别取﹣
、﹣
、﹣
、…、﹣
、﹣2、﹣1、0、1、2、…、2015、2016、2017时，计算分式
的值，再将所得结果相加，其和等于 ．
【答案】﹣
．
【解析】
试题分析：
=
=﹣
=﹣（1﹣
）=
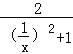﹣1把x是分数的情况代入，
=
=1﹣
把x是整数时代入，然后求值即可．
解：=
=﹣
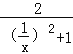=﹣（1﹣
）=
﹣1，
=
=1﹣
，
则当x=﹣
、﹣
、﹣
、…、﹣
时，代入后所得结果的和是【
﹣1】+【
﹣1】+…+【
﹣1】=
+
+…+
﹣2016，
x=﹣2、﹣1、0、1时，代入所得的式子的和是：【1﹣】+【1﹣
】+【1﹣
】+【1﹣】=
+0﹣1﹣0=﹣
．
当x=2、…、2015、2016、2017时，代入所得结果的和是【1﹣
】+…+【1﹣
】+【1﹣
】=+0+0﹣0﹣（+
+…+
+
）+2016=2016﹣（++…+
）
则x分别取﹣
、﹣
、﹣
、…、﹣
、﹣2、﹣1、0、1、2、…、2015、2016、2017时，计算分式
的值，再将所得结果相加是﹣．
故答案是：﹣．
练习册系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
