题目内容
【题目】如图,△ABC为等边三角形,D为BC延长线上的一点,以AD为边向形外作等边△ADE,连接CE.(1) 求证:△ACE≌△ABD;
(2) 在点D运动过程中,∠DCE的度数是否发生变化?若不变化,求它的度数;若变化,说明理由;
(3) 若∠BAE=150°,△ABD的面积为6,求四边形ACDE的面积.
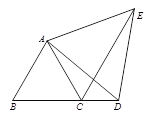
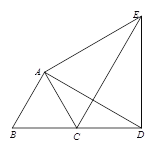
备用图
【答案】(1)证明见解析;(2)不发生变化,理由见解析;(3)12
【解析】试题分析:(1)易证AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,即可求得∠BAD=∠CAE,由全等三角形的判定SAS,证明△ABD≌△ACE;
(2)根据(1)知△ACE≌△ABD,然后根据全等三角形的性质和等边三角形性质,得出∠DCE=60°,得出不发生变化;
(3)根据(1)的结论,由∠BAE=150°,得到△ACE,△DCE,△ABD的面积相等,从而求出四边形的面积.
试题解析:(1) ∵△ABC为等边三角形,△ADE为等边三角形,∴∠ABC=∠ACB=60°,∠BAC=∠DAE=60°,AB=AC,AD=AE,∴∠BAC+∠DAC=∠DAC+∠DAE,即∠BAD=∠CAE.在△ACE与△ABD中,AB=AC,∠BAD=∠CAE,AD=AE,∴△ACE≌△ABD;
(2) 在点D运动过程中,∠DCE的度数不发生变化.理由如下:由(1)知:△ACE≌△ABD,∴∠ABC=∠ACE=60°.∵∠ACB=60°,∴∠ACD=120°,∠DCE=60°,∴在点D运动过程中,∠DCE的度数不发生变化.
(3)∵△ABC和△ADE是等边三角形
∴∠BAC=∠DAE=60°
∵∠BAE=150°
∴∠CAD=30°,∠BAD=90°,
∴∠BAD=30°
即△ACE≌△DCE
∵△ABD≌△ACE
∴四边形ACDE的面积=2△ACD的面积=2△ABD的面积=2×6=12.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案【题目】雾霾已经成为时下最普遍与敏感的话题.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了尚不完整的统计图表.
级别 | 观 点 | 频数(人数) |
A | 大气气压低,空气不流动 | 80 |
B | 地面灰尘大,空气湿度低 | m |
C | 汽车尾气排放 | n |
D | 工厂造成的污染 | 120 |
E | 其他 | 60 |

请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= ,扇形统计图中E组所占的百分比为 %;
(2)若该市人口约有100万人,请你估计其中持D组“观点”的市民人数.