ЬтФПФкШн
ЁОЬтФПЁПСНЬѕЦНаажБЯпЩЯИїга![]() ИіЕуЃЌгУет
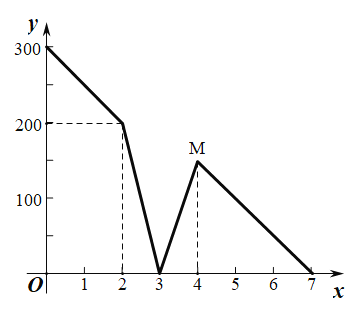
ИіЕуЃЌгУет![]() ЖдЕуАДШчЯТЕФЙцдђСЌНгЯпЖЮЃКЂйЦНааЯпжЎМфЕФЕудкСЌЯпЖЮЪБЃЌПЩвдгаЙВЭЌЕФЖЫЕуЃЌЕЋВЛФмгаЦфЫќНЛЕуЃЛЂкЗћКЯЂйвЊЧѓЕФЯпЖЮБиаыШЋВПЛГіЃЛЭМ1еЙЪОСЫЕБ
ЖдЕуАДШчЯТЕФЙцдђСЌНгЯпЖЮЃКЂйЦНааЯпжЎМфЕФЕудкСЌЯпЖЮЪБЃЌПЩвдгаЙВЭЌЕФЖЫЕуЃЌЕЋВЛФмгаЦфЫќНЛЕуЃЛЂкЗћКЯЂйвЊЧѓЕФЯпЖЮБиаыШЋВПЛГіЃЛЭМ1еЙЪОСЫЕБ![]() ЪБЕФЧщПіЃЌДЫЪБЭМжаШ§НЧаЮЕФИіЪ§ЮЊ0ЃЛЭМ2еЙЪОСЫЕБ
ЪБЕФЧщПіЃЌДЫЪБЭМжаШ§НЧаЮЕФИіЪ§ЮЊ0ЃЛЭМ2еЙЪОСЫЕБ![]() ЪБЕФвЛжжЧщПіЃЌДЫЪБЭМжаШ§НЧаЮЕФИіЪ§ЮЊ2ЃЛЭМ3еЙЪОСЫЕБ
ЪБЕФвЛжжЧщПіЃЌДЫЪБЭМжаШ§НЧаЮЕФИіЪ§ЮЊ2ЃЛЭМ3еЙЪОСЫЕБ![]() ЪБЕФвЛжжЧщПіЃЌДЫЪБЭМжаШ§НЧаЮЕФИіЪ§ЮЊ4ЃЛЪдВТЯыЕБ
ЪБЕФвЛжжЧщПіЃЌДЫЪБЭМжаШ§НЧаЮЕФИіЪ§ЮЊ4ЃЛЪдВТЯыЕБ![]() ЪБЃЌАДееЩЯЪіЙцдђЛГіЕФЭМаЮжаЃЌШ§НЧаЮзюЩйга____Иі
ЪБЃЌАДееЩЯЪіЙцдђЛГіЕФЭМаЮжаЃЌШ§НЧаЮзюЩйга____Иі

ЁОД№АИЁП4034
ЁОНтЮіЁП
ЗжЮіПЩЕУЃЌЕБn=1ЪБЕФЧщПіЃЌДЫЪБЭМжаШ§НЧаЮЕФИіЪ§ЮЊ0ЃЌга0=2ЃЈ1-1ЃЉЃЛЕБn=2ЪБЕФвЛжжЧщПіЃЌДЫЪБЭМжаШ§НЧаЮЕФИіЪ§ЮЊ2ЃЌга2=2ЃЈ2-1ЃЉЃЛЁЙЪЕБгаnЖдЕуЪБЃЌзюЩйПЩвдЛ2ЃЈn-1ЃЉИіШ§НЧаЮЃЛЕБn=2018ЪБЃЌАДЩЯЪіЙцдђЛГіЕФЭМаЮжаЃЌзюЩйга2ЁСЃЈ2018-1ЃЉ=4034ИіШ§НЧаЮЃЎ
ЕБn=1ЪБЕФЧщПіЃЌДЫЪБЭМжаШ§НЧаЮЕФИіЪ§ЮЊ0ЃЌга0=2ЃЈ1-1ЃЉЃЛЕБn=2ЪБЕФвЛжжЧщПіЃЌДЫЪБЭМжаШ§НЧаЮЕФИіЪ§ЮЊ2ЃЌга2=2ЃЈ2-1ЃЉЃЛЁЙЪЕБгаnЖдЕуЪБЃЌзюЩйПЩвдЛ2ЃЈn-1ЃЉИіШ§НЧаЮЃЛЕБn=2018ЪБЃЌ2ЁС(20181)= 4034Иі.

 дЦФЯЪІДѓИНаЁвЛЯпУћЪІЬсгХзївЕЯЕСаД№АИ
дЦФЯЪІДѓИНаЁвЛЯпУћЪІЬсгХзївЕЯЕСаД№АИ ГхДЬ100ЗжЕЅдЊгХЛЏСЗПМОэЯЕСаД№АИ
ГхДЬ100ЗжЕЅдЊгХЛЏСЗПМОэЯЕСаД№АИ