题目内容
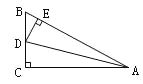
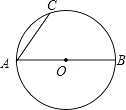
【题目】如图,已知AB=AC=AD,∠CAD=60°,分别连接BC、BD,作AE平分∠BAC交BD于点E,若BE=4,ED=8,则DF=_____.

【答案】6
【解析】
连接CE、CD,取DE的中点M,连接CM.首先证明△ECM,△ACD度数等边三角形,再证明△CEF∽△DEC即可解决问题.
解:连接CE、CD,取DE的中点M,连接CM.
∵AB=AC,∠EAB=∠EAC,AE=AE,
∴△EAB≌△EAC,
∴BE=EC=4,∠ABE=∠ACE,
∵AB=AD,
∴∠ABE=∠ADB,
∴∠ACE=∠ADF,
∵∠DFA=∠CFE,
∴∠DAF=∠CEF=60°,
∵EM=ED=4,
∴CE=EM,
∴△EMC是等边三角形,
∴CM=EM=DM,∠EMC=60°,
∵∠EMC=∠MCD+∠MDC,
∴∠MCD=∠MDC=30°,
∵AC=AD,∠CAD=60°,
∴△ACD是等边三角形,
∴∠ADC=60°,
∴∠ADB=∠ABD=∠ACE=∠CDB=30°,
∵∠CEF=∠CED,
∴△CEF∽△DEC,
∴EC2=EFED,
∴16=8EF,
∴EF=2,DF=DE﹣EF=6.
故答案为6.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
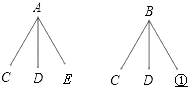
【题目】某电脑店有A、B两种型号的打印机和C、D、E三种芯片出售.每种型号的打印机均需要一种芯片配套才能打印.
(1)下列是该店用树形图或列表设计的配套方案,①的位置应填写 , ②的位置应 填写
(2)若仅有B型打印机与E种芯片不配套,则上面(1)中的方案配套成功率是
芯片 | C | D | E |
A | (A,C) | (A,D) | ② |
B | (B,C) | (B,D) | (B,E) |