题目内容
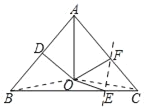
【题目】如图,在△ABC中,AB=AC,∠BAC=88°,∠BAC的平分线与AB的垂直平分线交于点O,点E、F分别在BC、AC上,点C沿EF折叠后与点O重合,则∠DOE的度数为_____.

【答案】140゜
【解析】
连接OB、OC,根据角平分线定义和线段垂直平分线的性质得到∠OAB=∠ABO=44°,再根据等腰三角形的性质得到∠ABC=∠ACB=46°,求出∠OBC=2°,由于AB=AC,OA平分∠BAC,根据等腰三角形的性质得OA垂直平分BC,则BO=OC,所以得出∠OBC=∠OCB=2°,然后根据折叠的性质得到EO=EC,于是∠OCB=∠EOC=2°,再根据三角形的外角性质得出∠OEB,求出∠BOE和∠BOD的度数,即可得出答案.
解:连接OB、OC,如图所示:
∵∠BAC=88°,∠BAC的平分线与AB的中垂线交于点O,
∴∠OAB=∠ABO=44°,
∵AB=AC,∠BAC=88°,
∴∠ABC=∠ACB=46°,
∴∠OBC=46°﹣44°=2°,
∵AB=AC,OA平分∠BAC,
∴OA垂直平分BC,
∴BO=OC,
∴∠OBC=∠OCB=2°,
∵点C沿EF折叠后与点O重合,
∴EO=EC,
∴∠OCB=∠EOC=2°,
∴∠OEB=∠OCB+∠EOC=4°,
∴∠BOE=180°﹣4°﹣2°=174°,
∵∠BOD=90°﹣44°=46°,
∴∠DOE=360°﹣46°﹣174°=140°,
故答案为:140°.

练习册系列答案
相关题目