题目内容
阅读下面材料:
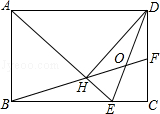
小腾遇到这样一个问题:如图1,在 中,点
中,点 在线段
在线段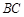 上,
上,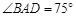 ,
,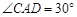 ,
,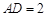 ,
,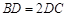 ,求
,求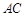 的长.
的长.
小腾发现,过点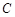 作
作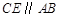 ,交
,交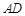 的延长线于点
的延长线于点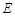 ,通过构造
,通过构造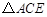 ,经过推理和计算能够使问题得到解决(如图2).
,经过推理和计算能够使问题得到解决(如图2).
请回答: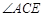 的度数为 ,
的度数为 ,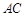 的长为 .
的长为 .
参考小腾思考问题的方法,解决问题:
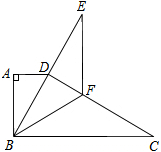
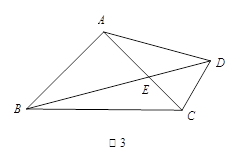
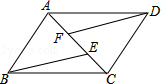
如图3,在四边形 中,
中,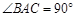 ,
,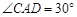 ,
,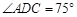 ,
,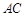 与
与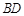 交于点
交于点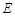 ,
,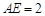 ,
,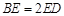 ,求
,求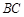 的长.
的长.
小腾遇到这样一个问题:如图1,在
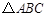 中,点
中,点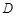 在线段
在线段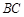 上,
上,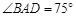 ,
,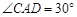 ,
,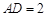 ,
,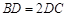 ,求
,求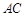 的长.
的长.
小腾发现,过点
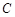 作
作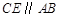 ,交
,交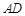 的延长线于点
的延长线于点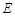 ,通过构造
,通过构造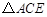 ,经过推理和计算能够使问题得到解决(如图2).
,经过推理和计算能够使问题得到解决(如图2).请回答:
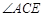 的度数为 ,
的度数为 ,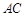 的长为 .
的长为 .参考小腾思考问题的方法,解决问题:
如图3,在四边形
 中,
中,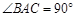 ,
,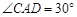 ,
,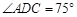 ,
,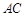 与
与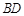 交于点
交于点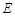 ,
,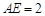 ,
,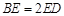 ,求
,求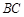 的长.
的长.
∠ACE的度数为75°,AC的长为3. 

试题分析:由CE//AB可知∠ACE=∠BAD=75°,又∠CAD=30°,可知△ACE是等腰三角形,又CE//AB可知△ABD∽△CED,由相似的性质可知DE=1,所以AD=AC=AE+CE=3
图3中,由已知的条件可知△ACD是等腰三角形,因为∠BAC=90°,因此可过点D作DF⊥AC,然后利用相似、三角函数、勾股定理加以解决
试题解析:图(2):∠ACE的度数为75°,AC的长为3.
图(3):过点D作DF⊥AC于F
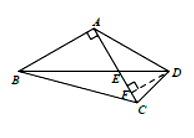
∵∠BAC=90°
∴AB//DF
∴△ABE∽△FDE
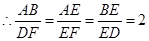
∴EF=1
∵在△ACD中,∠CAD=30°,∠ADC=75°
∴∠ACD=75°
∴AC=AD
∵DF⊥AC
∴∠AFD=90°
在△AFD中,AF=2+1=3,∠FAD=30°
∴DF=AFtan30°=
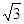 ,AD=2DF=2
,AD=2DF=2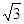
∴AC=2
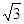 ,AB=2DF==2
,AB=2DF==2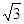


练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目

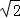 AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论: