题目内容
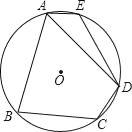
【题目】如图,四边形ABCD中,AB=3,BC=2,AC=AD,∠ACD=60°,则对角线BD长的最大值为( )
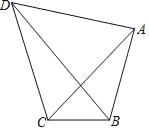
A. 5 B. 2![]() C. 2
C. 2![]() D. 1
D. 1
【答案】A
【解析】
在AB的左侧作等边三角形△ABK,连接DK.由△DAK≌△CAB,推出DK=BC=2,因为DK+KB≥BD,DK=2,KB=AB=3,所以当D、K、B共线时,BD的值最大,最大值为DK+KB=5.
如图,在AB的左侧作等边三角形△ABK,连接DK.
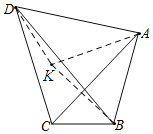
则AK=AB=BK=3,∠KAB=60°,
∴∠DAC=∠KAB,
∴∠DAK=∠CAB,
在△DAK和△CAB中,
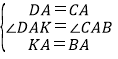 ,
,
∴△DAK≌△CAB(SAS),
∴DK=BC=2,
∵DK+KB≥BD,DK=2,KB=AB=3,
∴当D、K、B共线时,BD的值最大,最大值为DK+KB=5.
故选A.

练习册系列答案
相关题目
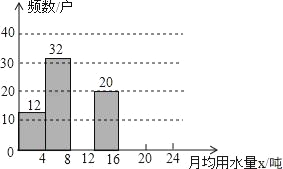
【题目】2014年,河北省委宣传部主办“河北节约之星”活动,表彰节水先进典型,省委宣传部号召全社会以节水先进典型为榜样,牢固树立节约用水理念,争做节俭美德的传承者,节约用水的践行者.小鹏想了解某小区住户月均用水情况,随机调查了该小区部分住户,并将调查数据绘制成如图所示的频数分布直方图(不完整)和如下的频数分布表.
月均用水量x(吨) | 频数(户) | 频率 |
0<x≤4 | 12 | a |
4<x≤8 | 32 | 0.32 |
8<x≤12 | b | c |
12<x≤16 | 20 | 0.2 |
16<x≤20 | 8 | 0.08 |
20<x≤24 | 4 | 0.04 |
(1)求a,b,c的值,并将如图所示的频数分布直方图补充完整;
(2)求月均用水量超过12吨的住户占所调查总住户的百分比;
(3)若该小区有1000住户,根据所调查的数据,该小区月均用水量没有超过8吨的住户有多少?