Question

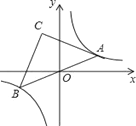
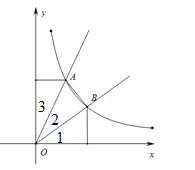
【题目】如图，以原点为端点的两条射线与反比例函数交于两点，且，则的面积是________.

Answer 1

【答案】

【解析】

由∠1=∠2=∠3，∠1+∠2+∠3=90°可得∠1=∠2=∠3=30°，再由特殊角的三角函数值、反比例函数比例系数|k| 可得S△AOD= S△EOB=3 ，S矩形ADOF=6，而S△AOD+ S△AOB+ S△EOB=S矩形ADOF+S梯形AFEB，A、B在双曲线上，所以S△AOD= S△EOB=3 ，S矩形ADOF=6

所以S△AOB= S梯形AFEB而S梯形AFEB=·FE= ·（OA-OA）

解得 S梯形AFEB==2 所以 的面积是2.

解：

如图所示，作AD⊥y轴于D，BE⊥x轴于E，AF⊥x轴于F，

∵∠1=∠2=∠3，∠1+∠2+∠3=90°

∴∠1=∠2=∠3=30°

∴A（OA，OA），B(OB，OB)

∵A、B在上

∴OA·OA=6，OB·OB =6

∴OA2= OB 2=8

∵S△AOD+ S△AOB+ S△EOB=S矩形ADOF+S梯形AFEB，A、B在双曲线上

∴S△AOD= S△EOB=3 ，S矩形ADOF=6

∴S△AOB= S梯形AFEB

而S梯形AFEB=·FE= ·（OA-OA）

∴ S梯形AFEB==2

的面积是2

故答案为：2.