题目内容
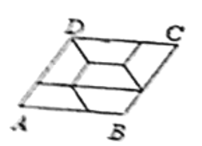
【题目】如图,菱形ABCD 由 6 个腰长为 2,且全等的等腰梯形镶嵌而成,则 AB 的长为_____________.
【答案】6
【解析】
根据AB=AD,得出等腰梯形的上底为2,再根据菱形的性质得出等腰梯形的底角为60°,进而根据已知线段长度得出上底与下底的和,即AB的长度.
解:∵四边形ABCD是菱形,
∴AB=AD
设等腰梯形的上底为a,下底为b,腰为c=2,
则由图可知,a+b=b+2,
∴a=2,
又∵AB∥DC,设等腰梯形的底角为x,
则x+2x=180°,
∴x=60°,
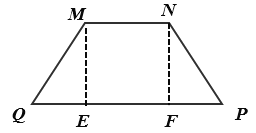
如下图,∠Q=60°,MN=MQ=2,作ME⊥PQ于点E,NF⊥PQ于点F,
则∠QME=30°,
∴QE=1,
则底边PQ为:1+1+2=4,
故AB的长度为:6.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目