题目内容
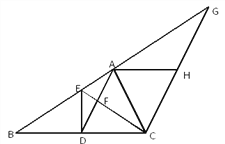
【题目】用硬纸板剪一个平行四边形ABCD,作出它的对角线的交点O,我们可以做如下操作:
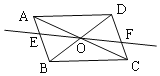
用大头针把一根平放在平行四边形上的直细木条固定在点O处,并使细木条可以绕点O转动,拨动细木条,它可以停留在任意位置. 如果设细木条与一组对边AB,CD的交点分别为点E,F,则下列结论:①OE=OF;②AE=CF;③BE=DF;④△AOE≌△COF,其中一定成立的是_________________________(填写序号即可).

【答案】①②③④.
【解析】
①④由四边形ABCD是平行四边形,可得AB∥DC,OA=OC,继而证得△AOE≌△COF(ASA),则可证①、④结论成立;②由△AOE≌△COF可得结论成立;③根据平行四边形的性质和②可得结论成立.
解:如图,直细木条所在直线与AB,CE分别交于点E,F.
①∵四边形ABCD是平行四边形,
∴AB∥DC,OA=OC,
∴∠BAO=∠DCO,
在△AOE和△COF中,
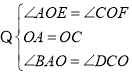
∴△AOE≌△COF(ASA),
∴OE=OF;
故①和④结论成立;
②由①知:△AOE≌△COF,
∴AE=CF,
故②结论成立;
③∵四边形ABFE为平行四边形;
∴AB=CD,
∵AE=CF,
∴BE=DF,
故③结论成立.
则一定成立的是:①②③④;
故答案为①②③④.

【题目】某超市销售每台进价分别为200元、150元的甲、乙两种型号的电器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
甲种型号 | 乙种型号 | ||
第一周 | 3台 | 5台 | 1900元 |
第二周 | 4台 | 10台 | 3200元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
⑴求A、B两种型号的电风扇的销售单价;
⑵若超市准备用不多于5000元的金额再采购这两种型号的电风扇共30台,且按(1)中的销售单价全部售完利润不少于1850元,则有几种购货方案?
⑶在⑵的条件下,超市销售完这30台电风扇哪种方案利润最大?最大利润是多少?请说明理由.