题目内容
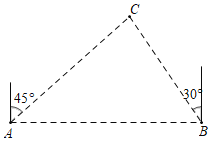
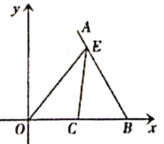
【题目】如图所示,在平面直角坐标系中,![]() ,
,![]() ,
,![]() 是等腰直角三角形且
是等腰直角三角形且![]() ,把
,把![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() ,得到
,得到![]() ,把
,把![]() 绕点C顺时针旋转
绕点C顺时针旋转![]() ,得到
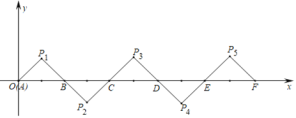
,得到![]() ,依此类推,得到的等腰直角三角形的直角顶点P2020的坐标为( )
,依此类推,得到的等腰直角三角形的直角顶点P2020的坐标为( )
A.(4039,-1)
B.(4039,1)
C.(2020,-1)
D.(2020,1)
【答案】A
【解析】
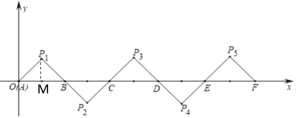
过点P1作P1M⊥x轴于M,先分别求出点P1、P2、P3、P4的坐标并找出横纵坐标的变化规律,然后归纳出点Pn的坐标,即可求出结论.
解:过点P1作P1M⊥x轴于M
∵![]() ,
,![]() ,
,![]() 是等腰直角三角形且
是等腰直角三角形且![]() ,
,
∴AM=P1M=![]() =1
=1
∴点P1的坐标为(1,1)=(2×1-1,(-1)1+1)
同理可得点P2的坐标为(3,-1)=(2×2-1, (-1)2+1)
点P3的坐标为(5,1)=(2×3-1, (-1)3+1)
点P4的坐标为(7,-1)=(2×4-1, (-1)4+1)
∴点Pn的坐标为(2n-1, (-1)n+1)
∴点P2020的坐标为(2×2020-1, (-1)2020+1)= (4039,-1)
故选A.

 阅读快车系列答案
阅读快车系列答案【题目】一方有难,八方支援.“新冠肺炎”疫情来袭,除了医务人员主动请缨逆行走向战场外,众多企业也伸出援助之手.某公司用甲,乙两种货车向武汉运送爱心物资,两次满载的运输情况如下表:
甲种货车辆数 | 乙种货车辆数 | 合计运物资吨数 | |
第一次 | 3 | 4 | 29 |
第二次 | 2 | 6 | 31 |
(1)求甲、乙两种货车每次满载分别能运输多少吨物资;
(2)目前有46.4吨物资要运输到武汉,该公司拟安排甲乙货车共10辆,全部物资一次运完,其中每辆甲车一次运送花费500元,每辆乙车一次运送花费300元,请问该公司应如何安排车辆最节省费用?
【题目】某印刷厂的打印机每5年需淘汰一批旧打印机并购买新机,买新机时,同时购买墨盒,每盒150元,每台新机最多可配买24盒;若非同时配买,则每盒需220元.
公司根据以往的记录,十台打印机正常工作五年消耗墨盒数如表:
消耗墨盒数 | 22 | 23 | 24 | 25 |
打印机台数 | 1 | 4 | 4 | 1 |
(1)以这十台打印机消耗墨盒数为样本,估计“一年该款打印机正常工作5年消耗的墨盒数不大于24”的概率;
(2)试以这10台打印机5年消耗的墨盒数的平均数作为决策依据,说明购买10台该款打印机时,每台应统一配买23盒墨还是24盒墨更合算?