题目内容
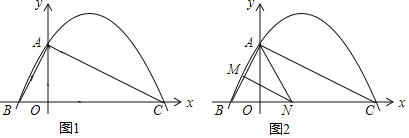
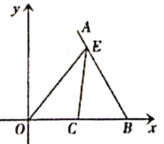
【题目】如图，在平面直角坐标系中，已知点
，
，
，
是线段
上的一个动点(点不与点
，
重合)．若
的值最小，则点的坐标为__________
【答案】（
，
）
【解析】
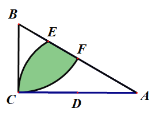
作点C关于AB的对称点F，连接OF，与AB相交于点E，则此时
的值最小，根据题意，求出直线AB的解析式，求出点F的坐标，然后求出直线OF的解析式，联合AB与OF，即可求出点E的坐标．
解：如图：作点C关于AB的对称点F，连接OF，与AB相交于点E，则此时的值最小，连接AC，CF与AB相交于点G，则点G是CF的中点；
∵点
，
，
，
∴AC⊥x轴，AC=3，BC=1，
∴AB=
，
设直线AB为
，
∴
，解得：
，
∴直线AB的解析式为：
，
设点G为（x，
），
∴
，
∵
，
∴
，
∴
，
解得：
，
∴
，
∴点G为（
，
），
∵点G是CF的中点，
∴点F为（
，
），
设直线OF为
，则
，解得：
，
∴直线OF为
，
∴联合直线AB和直线OF，则
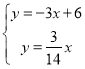，解得：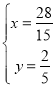
，
∴点E的坐标为（，）；
故答案为：（，）．
练习册系列答案
相关题目
