题目内容
【题目】数轴上点A,B对应的数分别是a,b,且a,b满足:![]() .
.
(1)填空:a= ,b= ;在数轴上描出点A,B;
(2)若点M在数轴上对应的数为m,且满足![]() ,则m= ;
,则m= ;
(3)若A,B两点同时沿数轴正方向匀速运动,点A的速度为每秒2个单位长度,点B的速度为每秒1个单位长度,在运动过程中,当点B到点O的距离是点A到点O距离的3倍时,点A对应的数是多少?
![]()
【答案】(1)-4;3;数轴表示见解析;(2)3;(3)2或![]() .
.
【解析】
(1)根据非负数的性质得出a、b的值,再在数轴上描点即可;
(2)分m<-6、m≥-6两种情况讨论去绝对值符号,再解所得方程即可;
(3)设运动时间为t,先用t表示出点A表示的数和点B表示的数,继而表示出OA、OB的长,然后根据点B到点O的距离是点A到点O距离的3倍列出方程,解方程即可.
解:(1)∵![]() ,
,
∴a+4=0且b-3=0,
解得:a=-4、b=3,
A,B的位置如图所示: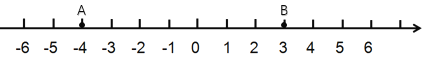
故答案为:-4;3;
(2)分类讨论解方程![]() ,
,
若m<-6,则2m-m-6=15,解得:m=21(不合题意,舍去);
若m≥-6时,2m+m+6=15,解得:m=3;
综上述,m=3,
故答案为:3;
(3)设t秒时,点B到点O的距离是点A到点O距离的3倍,
则此时点A表示的数为-4+2t,点B表示的数为3+t,
∴OA=|-4+2t|,OB=|3+t|,
∴3|-4+2t|=|3+t|,
∴3(-4+2t) =3+t或3(-4+2t) =-(3+t),
解得:t=3或t=![]() ,
,
当t=3时,-4+2t=![]() ,
,
当t=![]() 时,-4+2t=
时,-4+2t=![]() =
=![]() ,
,
∴点A对应的数为2或![]() .
.

【题目】某路公交车从起点经过A、B、C、D站到达终点,一路上下乘客如下表所示。(用正数表示上车的人数,负数表示下车的人数)
| 起点 | A | B | C | D | 终点 |
上车的人数 | 18 | 15 | 12 | 7 | 5 | 0 |
下车的人数 | 0 | -3 | -4 | -10 | -11 |
(1)到终点下车还有_________ 人;
(2)车行驶在那两站之间车上的乘客最多?_______站和________站;
(3)若每人乘坐一站需买票1元,问该车出车一次能收入多少钱?写出算式.