题目内容
【题目】如图，抛物线y=ax2+bx+c与x轴交于A（﹣1，0），B（4，0）与y轴交于点C（0，2），抛物线的对称轴交x轴于点D．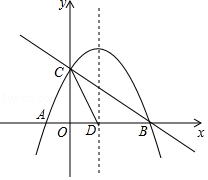
（1）求抛物线的表达式；
（2）在抛物线的对称轴是否存在点P，使△PCD是以CD为腰的等腰三角形，如果存在，求出P点的坐标，若不存在，请说明理由；
（3）点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？并求出四边形CDBF的最大面积及此时E点的坐标．
【答案】
（1）
解：把A（﹣1，0），B（4，0），C（0，2）代入y=ax2+bx+c中得：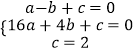 
，
解得： 
．
故抛物线的表达式为：y=﹣ 
x2+ 
x+2
（2）
解：y=﹣ x2+ x+2=﹣ （x﹣ ）2+ 
；
则D（ ，0），
在Rt△OCD中，OC=2，OD= ，
由勾股定理得：CD= 
= 
，
如图1，
①当CD=DP1时，△PCD是等腰三角形，
∴P1（ ， ），
②当CD=DP2时，△PCD是等腰三角形，
∴P2（ ，﹣ ），
③当CD=CP3时，△PCD是等腰三角形，
过C作CE⊥DP1于E，
∵C（0，2），
∴DE=OC=2，
∵CD=CP3，
∴DE=P3E=2，
∴P3（ ，4），
综上所述，P点的坐标为：P1（ ， ），P2（ ，﹣ ），P3（ ，4）
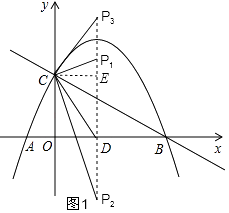
（3）
解：如图2，
∵A（﹣1，0），对称轴是：x= ，
∴B（4，0），
设BC的解析式为：y=kx+b，
把B（4，0），C（0，2）代入得： 
，
解得：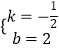 
，
∴BC的解析式为：y=﹣ x+2，
设E（m，﹣ m+2），F（m，﹣ m2+ m+2），
∴EF=﹣ m2+ m+2﹣（﹣ m+2）=﹣ m2+2m，
∴S四边形BDCF=S△BCD+S△BFC= BDOC+ EFOB= × ×2+ （﹣ m2+2m）×4，
S=﹣m2+4m+2.5=﹣（m﹣2）2+6.5（0＜m＜4），
当m=2时，﹣ m+2=﹣ ×2+2=1，
∴当m=2时，四边形CDBF的面积最大，最大为6.5，此时E（2，1）．
【解析】（1）利用待定系数法求抛物线的表达式；（2）以CD为腰的等腰三角形有三个：①②以D为圆心，以CD为半径画弧交对称轴于P1、P2 ， ③以C为圆心，以CD为半径画弧，交对称轴于P3 ， 分别求出这三个点的坐标；（3）先根据对称性求点B的坐标为（4，0），再求直线BC的解析式，设出点E和F的坐标，表示EF的长；则四边形BDCF的面积等于两个三角形面积的和，其中△BDC是定值，△BFC的面积=铅直高度与水平宽度的积，代入面积公式可求得S的解析式，求最值即可．
【考点精析】关于本题考查的坐标与图形变化-对称，需要了解关于x轴对称的点的特征：两个点关于x轴对称时，它们的坐标中，x相等，y的符号相反，即点P（x，y）关于x轴的对称点为P’（x，-y）；关于y轴对称的点的特征：两个点关于y轴对称时，它们的坐标中，y相等，x的符号相反，即点P（x，y）关于y轴的对称点为P’（-x，y）才能得出正确答案．
