Question

【题目】如图，已知长方形ABCD，AB＝1，BC＝2，点M为矩形内一点，点E为BC边上任意一点，则MA＋MD＋ME的最小值为( )

A. 1 B. 1+ C. 2+ D. 3

Answer 1

【答案】B

【解析】

将△AMD绕点A逆时针旋转60°得到△AM’D’，MD=M’D’，易得到△ADD’和△AMM’均为等边三角形，推出AM=MM’可得MA+MD+ME=D’M+MM’+ME，共线时最短；由于点E也为动点，可得当D’E⊥BC时最短，此时易求得D’E=DG+GE的值.

将△AMD绕点A逆时针旋转60°得到△AM’D’，MD=M’D’，易得到△ADD’和△AMM’均为等边三角形，

∴AM=MM’，

∴MA+MD+ME=D’M+MM’+ME，

∴D′M、MM′、ME共线时最短，

由于点E也为动点，

∴当D’E⊥BC时最短，此时易求得D’E=DG+GE=4+3，

∴MA+MD+ME的最小值为4+3．

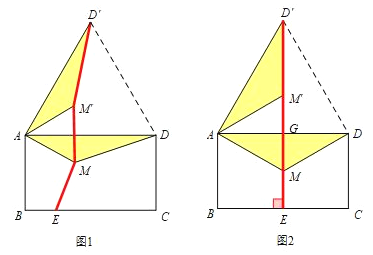
故选B．