题目内容
 两个大小不同的等腰直角三角形三角板如图所示放置,后一个图是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.
两个大小不同的等腰直角三角形三角板如图所示放置,后一个图是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.(1)求证:△ABE≌△ACD
(2)试猜想DC与BE的位置关系,并说明理由.
分析:(1)根据等腰直角三角形的性质以及全等三角形的判定即可得出△ABE≌△ACD;
(2)利用全等三角形的性质得出∠B=∠ACB=∠ACD=45°,进而得出∠DCB=90°,即可得出答案.
(2)利用全等三角形的性质得出∠B=∠ACB=∠ACD=45°,进而得出∠DCB=90°,即可得出答案.
解答:(1)证明:∵△ABC和△ADE都是等腰直角三角形,
∴AC=AB,AD=AE,∠BAC=∠EAD=90°,
∴∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD,
在△ABE和△ACD中,
∴
,
∴△ABE≌△ACD(SAS),
(2)解:DC与BE的位置关系是垂直关系.
证明:∵△ABE≌△ACD,
∴BE=CD,∠B=∠ACB=∠ACD=45°,
∴∠DCB=90°,
∴DC与BE的位置关系是垂直关系.
∴AC=AB,AD=AE,∠BAC=∠EAD=90°,
∴∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD,
在△ABE和△ACD中,
∴
|
∴△ABE≌△ACD(SAS),
(2)解:DC与BE的位置关系是垂直关系.
证明:∵△ABE≌△ACD,
∴BE=CD,∠B=∠ACB=∠ACD=45°,
∴∠DCB=90°,
∴DC与BE的位置关系是垂直关系.
点评:此题主要考查了等腰直角三角形的性质以及全等三角形的性质与判定,根据等腰三角形的性质得出AC=AB,AD=AE,利用SAS证全等是解题关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
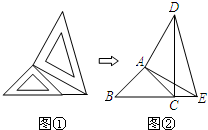 25、两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接CD.请找出图②中的全等三角形,并说明理由(说明:结论中不得含有未标识的字母).
25、两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接CD.请找出图②中的全等三角形,并说明理由(说明:结论中不得含有未标识的字母). 21、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.求证:
21、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.求证:

