题目内容
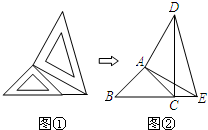25、两个大小不同的等腰直角三角形三角板如图①所示放置，图②是由它抽象出的几何图形，B，C，E在同一条直线上，连接CD．请找出图②中的全等三角形，并说明理由（说明：结论中不得含有未标识的字母）．分析：根据题意得AB=AC，AD=AE，∠BAC+∠CAE=∠DAE+∠CAE，即∠BAE=∠CAD，从而得出△ABE≌△ACD．
解答：解：图2中△ABE≌△ACD．理由如下：
∵△ABC与△AED都是直角三角形
∴∠BAC=∠EAD=90°（4分）
∴∠BAC+∠CAE=∠EAD+∠CAE即∠BAE=∠CAD（6分）
又∵AB=AC，AE=AD，
∴△ABE≌△ACD．（10分）
∵△ABC与△AED都是直角三角形
∴∠BAC=∠EAD=90°（4分）
∴∠BAC+∠CAE=∠EAD+∠CAE即∠BAE=∠CAD（6分）
又∵AB=AC，AE=AD，
∴△ABE≌△ACD．（10分）
点评：本题考查了等腰直角三角形的性质，全等三角形的判定和性质，培养学生发现问题的能力．
练习册系列答案
相关题目
21、两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B，C，E在同一条直线上，连接DC．求证：
