题目内容
两个大小不同的等腰直角三角板,如图1所示:

(1)若两个等腰直角三角板如图2放置,求证:EC⊥BD.
(2)若两个等腰直角三角板如图3放置,使B、C、D在同一条直线上,连接EC交AD于点M,你认为EC与BD是否仍然垂直?请说明理由.

(1)若两个等腰直角三角板如图2放置,求证:EC⊥BD.
(2)若两个等腰直角三角板如图3放置,使B、C、D在同一条直线上,连接EC交AD于点M,你认为EC与BD是否仍然垂直?请说明理由.
分析:(1)根据等腰直角三角形性质得出AE=AD,AM=AB,∠EAD=∠MAB=90°,证△EAM≌△DAB,推出∠AEM=∠ADB,根据∠DAB=90°求出∠DBA+∠MEA=90°,求出∠ECB=90°,即可得出答案;
(2)根据等腰直角三角形的性质得出∴AE=AD,AC=AB,∠EAD=∠CAB=90°,求出∠EAC=∠BAD,证△EAC≌△DAB,推出∠CEA=∠ADB,求出∠ECD=90°即可.
(2)根据等腰直角三角形的性质得出∴AE=AD,AC=AB,∠EAD=∠CAB=90°,求出∠EAC=∠BAD,证△EAC≌△DAB,推出∠CEA=∠ADB,求出∠ECD=90°即可.
解答:(1)证明:
∵△EAD和△MAB是等腰直角三角形,
∴AE=AD,AM=AB,∠EAD=∠MAB=90°,
在△EAM和△DAB中
∴△EAM≌△DAB(SAS),
∴∠AEM=∠ADB,
∵∠DAB=90°,
∴∠DBA+∠ADB=90°,
∴∠DBA+∠MEA=90°,
∴∠ECB=180°-90°=90°,
∴EC⊥BD;
(2)解:EC⊥BD,
理由是:∵△EAD和△CAB是等腰直角三角形,
∴AE=AD,AC=AB,∠EAD=∠CAB=90°,
∴∠EAM+∠DAC=∠BCA+∠DAC,
∴∠EAC=∠BAD,
在△EAC和△DAB中
∴△EAC≌△DAB(SAS),
∴∠CEA=∠ADB,
∵∠EAM=90°,
∴∠CEA+∠EMA=90°,
∵∠EMA=∠DMC,
∴∠DMC+∠BDA=90°,
∴∠ECD=180°-90°=90°,
∴EC⊥BD.
∵△EAD和△MAB是等腰直角三角形,
∴AE=AD,AM=AB,∠EAD=∠MAB=90°,
在△EAM和△DAB中
|
∴△EAM≌△DAB(SAS),
∴∠AEM=∠ADB,
∵∠DAB=90°,
∴∠DBA+∠ADB=90°,
∴∠DBA+∠MEA=90°,
∴∠ECB=180°-90°=90°,
∴EC⊥BD;
(2)解:EC⊥BD,
理由是:∵△EAD和△CAB是等腰直角三角形,
∴AE=AD,AC=AB,∠EAD=∠CAB=90°,
∴∠EAM+∠DAC=∠BCA+∠DAC,
∴∠EAC=∠BAD,
在△EAC和△DAB中
|
∴△EAC≌△DAB(SAS),
∴∠CEA=∠ADB,
∵∠EAM=90°,
∴∠CEA+∠EMA=90°,
∵∠EMA=∠DMC,
∴∠DMC+∠BDA=90°,
∴∠ECD=180°-90°=90°,
∴EC⊥BD.
点评:本题考查了等腰直角三角形性质,三角形的内角和定理,全等三角形的性质和判定的应用,主要考查学生的推理能力,此题证明过程类似.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
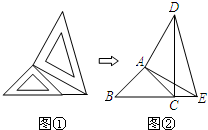 25、两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接CD.请找出图②中的全等三角形,并说明理由(说明:结论中不得含有未标识的字母).
25、两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接CD.请找出图②中的全等三角形,并说明理由(说明:结论中不得含有未标识的字母). 21、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.求证:
21、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.求证:
