Question

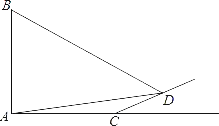
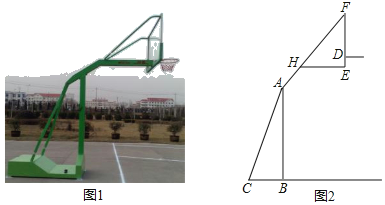
【题目】如图是某种品牌的篮球架实物图与示意图，已知底座BC＝0.6米，底座BC与支架AC所成的角∠ACB＝75°，支架AF的长为2.5米，篮板顶端F点到篮框D的距离FD＝1.4米，篮板底部支架HE与支架AF所成的角∠FHE＝60°，求篮框D到地面的距离．（精确到0.1米．参考数据：cos75°≈0.3，sin75°≈0.9，．tan75°≈3.7，≈1.7，≈1.4）

Answer 1

【答案】篮框D到地面的距离是2.9米．

【解析】

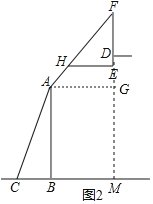
延长FE交CB的延长线于M，过A作AG⊥FM于G，解直角三角形即可得到结论．

解：延长FE交CB的延长线于M，过A作AG⊥FM于G，

在Rt△ABC中，tan∠ACB＝

∴AB＝BCtan75°＝0.60×3.732＝2.22，

∴GM＝AB＝2.22，

在Rt△AGF中，∵∠FAG＝∠FHE＝60°，sin∠FAG＝

∴sin60°＝

∴FG＝2.125，

∴DM＝FG+GM﹣DF≈2.9米．

答：篮框D到地面的距离是2.9米．