题目内容
【题目】如图，D是△ABC的边BC上一点，AB＝4，AD＝2，∠DAC＝∠B，如果△ABD的面积为15，那么△ACD的面积为( )
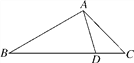
A. 15 B. 10 C. 
D. 5
【答案】D
【解析】首先证明△ACD∽△BCA，由相似三角形的性质可得：△ACD的面积：△ABC的面积为1：4，因为△ABD的面积为9，进而求出△ACD的面积．
解：∵∠DAC=∠B，∠C=∠C，∴△ACD∽△BCA，∵AB=4，AD=2，∴△ACD的面积：△ABC的面积为1：4，∴△ACD的面积：△ABD的面积=1：3，∵△ABD的面积为15，
∴△ACD的面积∴△ACD的面积=5．
故选D．
“点睛”本题考查了相似三角形的判定和性质：相似三角形的面积比等于相似比的平方，是中考常见题型．
练习册系列答案
计算高手系列答案
相关题目