题目内容
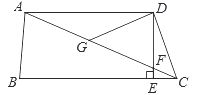
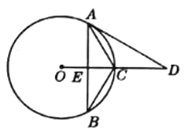
【题目】△ABC中,AB=AC=5,BC=6,过AB上一点D作DE‖BC,DF‖AC分别交AC、BC于点E和F

(1)如图1,证明:△ADE∽△DBF;
(2)如图1,若四边形DECF是菱形,求DE的长;
(3)如图2,若以D、E、F为顶点的三角形与△BDF相似,求AD的长.
【答案】(1)见解析;(2)DE的长为![]() ;(3)AD的长为
;(3)AD的长为![]() 或
或![]() .
.
【解析】
(1)根据平行线的性质得∠ADE=∠B,∠A=∠BDF,则根据相似三角形的判定方法可判断△ADE∽△DBF;
(2)设DE=x,利用菱形的性质得DE=DF=CF=CE=x,则AE=5﹣x,BF=6﹣x,根据相似三角形的性质得![]() =
=![]() ,即
,即![]() =
=![]() ,然后利用相似比的性质求出x即可;
,然后利用相似比的性质求出x即可;
(3)设AD=AE=t,则CE=5﹣t,先判断四边形DECF为平行四边形,所以DF=CE=5﹣t,DE=CF,利用平行线分线段成比例的性质可表示出DE=![]() t,则CF=
t,则CF=![]() t,BF=6﹣
t,BF=6﹣![]() t,由于∠EDF=∠BFD,根据相似三角形的判定方法,当
t,由于∠EDF=∠BFD,根据相似三角形的判定方法,当![]() =
=![]() ,△EDF∽△BFD,即BF=DE,6﹣
,△EDF∽△BFD,即BF=DE,6﹣![]() t=
t=![]() t;当
t;当![]() =
=![]() ,△EDF∽△DFB,即
,△EDF∽△DFB,即![]() =
=![]() ,然后利用比例性质分别求出t即可.
,然后利用比例性质分别求出t即可.
(1)证明:∵DE‖BC,DF‖AC,
∴∠ADE=∠B,∠A=∠BDF,
∴△ADE∽△DBF;
(2)解:设DE=x,
∵四边形DECF是菱形,
∴DE=DF=CF=CE=x,
∴AE=5﹣x,BF=6﹣x,
∵△ADE∽△DBF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得x=
,解得x=![]() ,
,
即DE的长为![]() ;
;
(3)解:设AD=AE=t,则CE=5﹣t,
∵DE‖BC,DF‖AC,
∴四边形DECF为平行四边形,
∴DF=CE=5﹣t,DE=CF,
∵DE∥BC,
∵![]() =
=![]() ,即
,即![]() =
=![]() ,则DE=
,则DE=![]() t,
t,
∴CF=![]() t,
t,
∴BF=6﹣![]() t,
t,
∵∠EDF=∠BFD,
∴当![]() =
=![]() ,△EDF∽△BFD,即BF=DE,6﹣
,△EDF∽△BFD,即BF=DE,6﹣![]() t=
t=![]() t,解得t=
t,解得t=![]() ;
;
当![]() =
=![]() ,△EDF∽△DFB,即
,△EDF∽△DFB,即![]() =
=![]() ,解得t=5(舍去)或t=
,解得t=5(舍去)或t=![]() ,
,
综上所述,AD的长为![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案