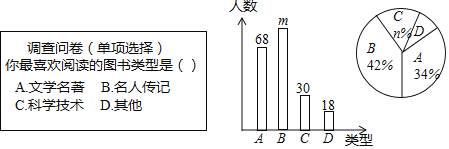
题目内容
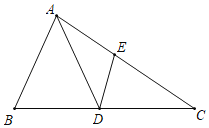
【题目】如图,在![]() 中,点
中,点![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,且
,且![]() .
.
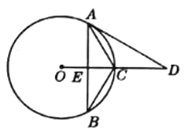
(1)求证![]() 与
与![]() 相切;
相切;
(2)若![]() ,求弦
,求弦![]() 的长.
的长.
【答案】(1)证明见详解
(2)AB=![]()
【解析】
第一问,求证AD与![]() 相切,就需要连接AO,求出∠OAD=90°,利用C点为
相切,就需要连接AO,求出∠OAD=90°,利用C点为![]() 的中点,且
的中点,且![]() ,得到∠OCA=60°,进而得到∠OAC=60°,利用△ACB得到∠ABC=30°
,得到∠OCA=60°,进而得到∠OAC=60°,利用△ACB得到∠ABC=30°
且利用∠B=∠D,得到∠DAC=30°,最后就能得到∠OAD=90°
第二问,利用解直角三角形方法,求解△AEC,可以得到AE的长,然后就能得出AB的长
解:(1)连接OA,∵∠ACB=120°,且点C为![]() 的中点,又垂径定理可知,CO⊥AB,且平分AB,∴AE=BE,∠AEC=∠BEC,EC=EC,∴
的中点,又垂径定理可知,CO⊥AB,且平分AB,∴AE=BE,∠AEC=∠BEC,EC=EC,∴![]() ,∴∠ACE=60°,AC=BC,∴∠CAB=∠B=30°,∠ACD=12°,∵∠B=∠D=30°,∴∠CAD=30°,∵OC=OA,
,∴∠ACE=60°,AC=BC,∴∠CAB=∠B=30°,∠ACD=12°,∵∠B=∠D=30°,∴∠CAD=30°,∵OC=OA,
∴∠OAC=∠OCA=60°,∴∠OAD=90°,∴![]() 与
与![]() 相切.
相切.
(2)AE=CE×tan∠ACE=![]() ,AB=2AE=
,AB=2AE=![]()


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,顺风车行经营的![]() 型车去年6月份销售总额为3.2万元,今年经过改造升级后
型车去年6月份销售总额为3.2万元,今年经过改造升级后![]() 型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的
型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的![]() 型车数量相同,则今年6月份
型车数量相同,则今年6月份![]() 型车销售总额将比去年6月份销售总额增加
型车销售总额将比去年6月份销售总额增加![]() .
.
![]() ,
,![]() 两种型号车的进货和销售价格表:
两种型号车的进货和销售价格表:
|
| |
进货价格(元 | 1100 | 1400 |
销售价格(元 | 今年的销售价格 | 2400 |
(1)求今年6月份![]() 型车每辆销售价多少元;
型车每辆销售价多少元;
(2)该车行计划7月份新进一批![]() 型车和
型车和![]() 型车共50辆,且
型车共50辆,且![]() 型车的进货数量不超过
型车的进货数量不超过![]() 型车数量的两倍,应如何进货才能使这批车获利最多?
型车数量的两倍,应如何进货才能使这批车获利最多?