题目内容
已知:二次函数y=x2-4x-a,下列说法中错误的个数是( )
①若图象与x轴有交点,则a≤4
②若该抛物线的顶点在直线y=2x上,则a的值为-8
③当a=-3时,不等式x2-4x+a>0的解集是1<x<3
④若将图象向上平移1个单位,再向左平移3个单位后过点(1,-2),则a=-1
⑤若抛物线与x轴有两个交点,横坐标分别为x1、x2,则当x取x1+x2时的函数值与x取0时的函数值相等.
①若图象与x轴有交点,则a≤4
②若该抛物线的顶点在直线y=2x上,则a的值为-8
③当a=-3时,不等式x2-4x+a>0的解集是1<x<3
④若将图象向上平移1个单位,再向左平移3个单位后过点(1,-2),则a=-1
⑤若抛物线与x轴有两个交点,横坐标分别为x1、x2,则当x取x1+x2时的函数值与x取0时的函数值相等.
分析:①和x轴有交点,就说明△≥0,易求a的取值;
②求出二次函数定点的表达式,代入直线解析式即可求出a的值;
③将a=3代入不等式,即可求其解集;
④将解析式化为顶点式,利用解析式平移的规律解答;
⑤利用根与系数的关系将x1+x2的值代入解析式进行计算即可.
②求出二次函数定点的表达式,代入直线解析式即可求出a的值;
③将a=3代入不等式,即可求其解集;
④将解析式化为顶点式,利用解析式平移的规律解答;
⑤利用根与系数的关系将x1+x2的值代入解析式进行计算即可.
解答:解:①当△=b2-4ac=16+4a≥0,即a≥-4时,二次函数和x轴有交点,故①错误;
②∵二次函数y=x2-4x-a的顶点坐标为(2,a-4),代入y=2x得,a-4=2×2,a=8,故②错误;
③当a=3时,y=x2-4x+3,图象与x轴交点坐标为:(1,0),(3,0),
故不等式x2-4x+a>0的解集是:x<1或x>3,故③错误;
④将图象向上平移1个单位,再向左平移3个单位后解析式为:y=(x+1)2+a-3,
∵图象过点(1,-2),∴将此点代入得:-2=(1+1)2+a-3,解得:a=-3.故④正确;
⑤由根与系数的关系,x1+x2=4,
当x=4时,y=16-16+a=a,
当x=0时,y=a,故⑤正确.
故选:B.
②∵二次函数y=x2-4x-a的顶点坐标为(2,a-4),代入y=2x得,a-4=2×2,a=8,故②错误;
③当a=3时,y=x2-4x+3,图象与x轴交点坐标为:(1,0),(3,0),
故不等式x2-4x+a>0的解集是:x<1或x>3,故③错误;
④将图象向上平移1个单位,再向左平移3个单位后解析式为:y=(x+1)2+a-3,
∵图象过点(1,-2),∴将此点代入得:-2=(1+1)2+a-3,解得:a=-3.故④正确;
⑤由根与系数的关系,x1+x2=4,
当x=4时,y=16-16+a=a,
当x=0时,y=a,故⑤正确.
故选:B.
点评:此题考查了抛物线与x轴的交点、根与系数的关系、二次函数图象与几何变换、待定系数法求二次函数解析式、二次函数与不等式(组)等知识,综合性较强.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.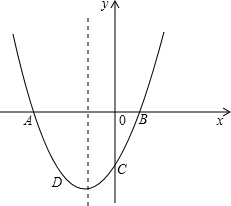 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.