题目内容
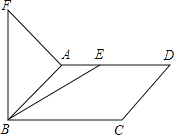
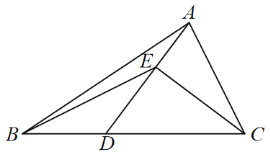
【题目】如图,在![]() 中,
中,![]() 是
是![]() 边上的点,连接
边上的点,连接![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,则线段
,则线段![]() 的长为____________.
的长为____________.
【答案】![]()
【解析】
过点A、E分别作AF⊥CD,EH⊥CD,垂足分别为点F、H,先根据![]() 证得AD=CD,进而可证得△ADF≌△CDE,得AF=CE,DF=DE=3,再根据
证得AD=CD,进而可证得△ADF≌△CDE,得AF=CE,DF=DE=3,再根据![]() ,设AF=CE=2x,则AB=
,设AF=CE=2x,则AB=![]() x,利用勾股定理BF=3x,进而可表示出BD=3x-3,AE=2x-2,AD=2x+1,再根据勾股定理列出方程求得x的值,最后再证明△DEH∽△DAF,进而可根据相似三角形的性质得到DH和EH的长,进而可求得BE的长.
x,利用勾股定理BF=3x,进而可表示出BD=3x-3,AE=2x-2,AD=2x+1,再根据勾股定理列出方程求得x的值,最后再证明△DEH∽△DAF,进而可根据相似三角形的性质得到DH和EH的长,进而可求得BE的长.
解:如图,过点A、E分别作AF⊥CD,EH⊥CD,垂足分别为点F、H,
∵![]() ,
,
∴![]() ,
,
∵CE⊥AD,AF⊥CD,
∴∠AEC=∠CED=∠AFD=90°,
∴![]() ,
,
∴![]() ,
,
即∠ACB=∠DAC,
∴AD=CD,
∴在△ADF与△CDE中,

∴△ADF≌△CDE(AAS)
∴AF=CE,DF=DE=3,
∵![]() ,
,
∴设AF=CE=2x,则AB=![]() x,
x,
在Rt△ABF中,BF=![]() ,
,
∴BD=BF-DF=3x-3,
∵![]() ,
,
∴![]() ,
,
∴AD=AE+DE=2x-2+3=2x+1,
在Rt△ADF中,![]() ,
,
∴![]() ,
,
解得:x=2,
∴AF=CE=2x=4,AD=2x+1=5,BD=3x-3=3,
∵AF⊥CD,EH⊥CD,
∴AF∥EH,
∴△DEH∽△DAF,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() ,
,
在Rt△BHE中,![]() ,
,
故答案为:![]() .
.


练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目