题目内容
【题目】如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上运动,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若∠B′ED=90°,则BD的长是________.

【答案】5
【解析】试题分析:如图,当点E与C重合时,∠B′ED=90°,设BD=x,由折叠得:B′D=x,CD=8-x,B′C=10-6=4,根据勾股定理列方程即可.
解:当∠B′ED=90°时,如图所示,点E与C重合,
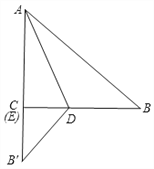
设BD=x,则CD=8x,
由折叠得:B′D=x,
∵∠ACB=90°,AC=6,BC=8,
∴AB=10,
∴AB′=AB=10,
∴B′C=106=4,
在Rt△CDB′中,B′D2=B′C2+CD2,
则x2=42+(8x)2,
解得x=5,
∴BD=5,
故答案为:5.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目