题目内容
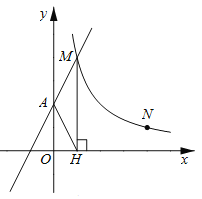
【题目】如图，直线
与
轴交于A点，与反比例函数
的图象交于点M，过M作MH⊥
轴于点H，且tan∠AHO=2.
（1）求
的值；
（2）在
轴上是否存在点P，使以点P、A、H、M为顶点的四边形是平行四边形？如果存在，直接写出P点坐标；如果不存在，请说明理由．
（3）点N（
，1）是反比例函数图象上的点，在x轴上有一点P，使得PM+PN最小，请求出点P的坐标.
【答案】（1）4；（2）存在；P点坐标为（0，6）或（0，-2）；（3）（
，0）．
【解析】
试题分析：（1）对于y=2x+2，令x=0求出y的值，确定出A的坐标，得到OA的长，根据tan∠AHO的值，利用锐角三角函数定义求出OH的长，根据MH垂直于x轴，确定出M横坐标，代入直线解析式求出纵坐标，确定出M的坐标，代入反比例解析式求出k的值即可；
（2）存在，理由为：如图所示，分两种情况考虑：当四边形P1AHM为平行四边形时；当四边形AP2HM为平行四边形时，利用平行四边形的性质确定出P的坐标即可；
（3）把M坐标代入反比例解析式求出a的值，确定出N坐标，过点N作N关于x轴的对称点N1，连接MN1，交x轴于P，此时PM+PN最小，利用待定系数法确定出直线MN1的解析式，即可确定出P的坐标．
试题解析：（1）由y=2x+2可知A（0，2），即OA=2，
∵tan∠AHO=2，
∴OH=1，
∵MH⊥x轴，
∴点M的横坐标为1，
∵点M在直线y=2x+2上，
∴点M的纵坐标为4，即M（1，4），
∵点M在y=
上，
∴k=1×4=4；
（2）存在，如图所示：
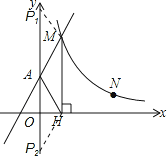
当四边形P1AHM为平行四边形时，P1A=MH=4，
∴P1A+AO=4+2=6，即P1（0，6）；
当四边形AP2HM为平行四边形时，MH=AP2=4，
∴OP2=AP2-OA=4-2=2，此时P2（0，-2），
综上，P点坐标为（0，6）或（0，-2）；
（3）∵点N（a，1）在反比例函数y=上，
∴a=4，即点N的坐标为（4，1），
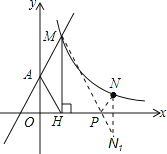
过点N作N关于x轴的对称点N1，连接MN1，交x轴于P，此时PM+PN最小，
∵N与N1关于x轴的对称，N点坐标为（4，1），
∴N1的坐标为（4，-1），
设直线MN1的解析式为y=kx+b，
由
，解得：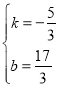
，
∴直线MN1的解析式为y=-
x+
，
令y=0，得x=，
∴P点坐标为（，0）．
