题目内容
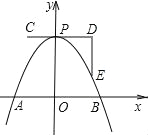
【题目】如图，一条抛物线与x轴相交于A、B两点，其顶点P在折线C-D-E上移动，若点C、D、E的坐标分别为（-1，4）、（3，4）、（3，1），点B的横坐标的最小值为1，则点A的横坐标的最大值为（ ）
A．1 B．2 C．3 D．4
【答案】B.
【解析】
试题解析：由图知：当点B的横坐标为1时，抛物线顶点取C（-1，4），设该抛物线的解析式为：y=a（x+1）2+4，代入点B坐标，得：
0=a（1+1）2+4，a=-1，
即：B点横坐标取最小值时，抛物线的解析式为：y=-（x+1）2+4．
当A点横坐标取最大值时，抛物线顶点应取E（3，1），则此时抛物线的解析式：y=-（x-3）2+1=-x2+6x-8=-（x-2）（x-4），即与x轴的交点为（2，0）或（4，0）（舍去），
∴点A的横坐标的最大值为2．
故选B．
练习册系列答案
阅读快车系列答案
相关题目
