��Ŀ����
���Ķ����в��ϣ����⣺��֪����x2+x-3=0����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸���2���⣺�����̵ĸ�Ϊy����y=2x��
����x=
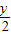 ��
����x=
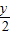 ������֪���̣���
������֪���̣���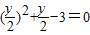
����y2+2y-12=0������Ϊy2+2y-12=0��
�������÷��̸��Ĵ������·��̵ķ��������dz�Ϊ������������
��1����֪����x2+x-1=0����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸���3����������Ϊ______
��2����֪����x��һԪ���η���ax2+bx+c=0���������������ʵ��������һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸��ĵ�����
��3����֪����x�ķ���x2-mx+n=0������ʵ��������һ�����̣�ʹ���ĸ��ֱ�����֪���̸���ƽ����
���𰸡����������������IJ��ϣ������̵ĸ�Ϊy���ٱ�ʾ��x������ԭ���̣��������ɵó�����ķ��̣�
����⣺��1�������̵ĸ�Ϊy����y=3x��
����x= ��
��
��x= ������֪���̣���
������֪���̣���

����y2+3y-9=0��
������Ϊy2+3y-9=0��
�ʴ��ǣ�y2+3y-9=0��
��2�������̵ĸ�Ϊy����y= ��x��0��������x=
��x��0��������x= ��y��0��
��y��0��
��x= ���뷽��ax2+bx+c=0����a��
���뷽��ax2+bx+c=0����a��  ��2+b•
��2+b• +c=0
+c=0
ȥ��ĸ����a+by+cy2=0��
��c=0����ax2+bx=0�����Ƿ���ax2+bx+c=0��һ����Ϊ0�����������⣬
��c��0��
������Ϊcy2+by+a=0��c��0����
��3�������̵ĸ�Ϊy����y=x2��
����x=± ��
��
�ٵ�x= ʱ��
ʱ��
��x=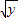 ������֪���̣���
������֪���̣���
 -m
-m +n=0����y-m
+n=0����y-m +n=0��
+n=0��
�ڵ�x=- ʱ��
ʱ��
��x=- ������֪���̣���
������֪���̣���
 +m
+m +n=0����y+m
+n=0����y+m +n=0��
+n=0��
������������Ҫ������һԪ���η��̵Ľ⡢�����б�ʽ��������һ�������⣬��һ���������⣬����ʱ��Ҫ��ȡ�����еĹؼ�����Ϣ��
����⣺��1�������̵ĸ�Ϊy����y=3x��
����x=
 ��
����x=
 ������֪���̣���
������֪���̣���
����y2+3y-9=0��
������Ϊy2+3y-9=0��
�ʴ��ǣ�y2+3y-9=0��
��2�������̵ĸ�Ϊy����y=
 ��x��0��������x=
��x��0��������x= ��y��0��
��y��0����x=
 ���뷽��ax2+bx+c=0����a��
���뷽��ax2+bx+c=0����a��  ��2+b•
��2+b• +c=0
+c=0ȥ��ĸ����a+by+cy2=0��
��c=0����ax2+bx=0�����Ƿ���ax2+bx+c=0��һ����Ϊ0�����������⣬
��c��0��
������Ϊcy2+by+a=0��c��0����
��3�������̵ĸ�Ϊy����y=x2��
����x=±
 ��
���ٵ�x=
 ʱ��
ʱ����x=
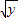 ������֪���̣���
������֪���̣��� -m
-m +n=0����y-m
+n=0����y-m +n=0��
+n=0���ڵ�x=-
 ʱ��
ʱ����x=-
 ������֪���̣���
������֪���̣��� +m
+m +n=0����y+m
+n=0����y+m +n=0��
+n=0��������������Ҫ������һԪ���η��̵Ľ⡢�����б�ʽ��������һ�������⣬��һ���������⣬����ʱ��Ҫ��ȡ�����еĹؼ�����Ϣ��

��ϰ��ϵ�д�
 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
�����Ŀ

 ���Ķ����в��ϣ�
���Ķ����в��ϣ�