题目内容
 请阅读下列材料:
请阅读下列材料:问题:正方形ABCD中,M,N分别是直线CB、DC上的动点,∠MAN=45°,当∠MAN交边CB、DC于点M、N(如图①)时,线段BM、DN和MN之间有怎样的数量关系?
小聪同学的思路是:延长CB至E使BE=DN,并连接AE,构造全等三角形经过推理使问题得到解决.请你参考小聪同学的思路,探究并解决下列问题:
(1)直接写出上面问题中,线段BM,DN和MN之间的数量关系;
(2)当∠MAN分别交边CB,DC的延长线于点M/N时(如图②),线段BM,DN和MN之间的又有怎样的数量关系?请写出你的猜想,并加以证明;
(3)在图①中,若正方形的边长为16cm,DN=4cm,请利用(1)中的结论,试求MN的长.
分析:(1)根据小聪同学的思路,可证△ABE与△ADN全等,从而证明△AMN与△AME全等,得关系式;
(2)在DC上截取DF=BM,得△ABM与△ADF全等;再证明△MAN与△FAN全等,得关系式;
(3)运用勾股定理计算.
(2)在DC上截取DF=BM,得△ABM与△ADF全等;再证明△MAN与△FAN全等,得关系式;
(3)运用勾股定理计算.
解答: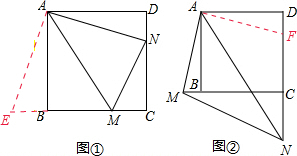 解:(1)BM+DN=MN;
解:(1)BM+DN=MN;
(2)DN-BM=MN.
理由如下:
如图,在DC上截取DF=BM,连接AF.
∵AB=AD,∠ABM=∠ADF=90°,
∴△ABM≌△ADF (SAS)
∴AM=AF,∠MAB=∠FAD.
∴∠MAB+∠BAF=∠FAD+∠BAF=90°,
即∠MAF=∠BAD=90°.
又∠MAN=45°,
∴∠NAF=∠MAN=45°.
∵AN=AN,
∴△MAN≌△FAN.
∴MN=FN,
即 MN=DN-DF=DN-BM;
(3)∵正方形的边长为16,DN=4,
∴CN=12.
根据(1)可知,BM+DN=MN,
设 MN=x,则 BM=x-4,
∴CM=16-(x-4)=20-x.
在Rt△CMN中,
∵MN2=CM2+CN2,
∴x2=(20-x)2+122.
解得 x=13.6.
∴MN=13.6cm.
 解:(1)BM+DN=MN;
解:(1)BM+DN=MN;(2)DN-BM=MN.
理由如下:
如图,在DC上截取DF=BM,连接AF.
∵AB=AD,∠ABM=∠ADF=90°,
∴△ABM≌△ADF (SAS)
∴AM=AF,∠MAB=∠FAD.
∴∠MAB+∠BAF=∠FAD+∠BAF=90°,
即∠MAF=∠BAD=90°.
又∠MAN=45°,
∴∠NAF=∠MAN=45°.
∵AN=AN,
∴△MAN≌△FAN.
∴MN=FN,
即 MN=DN-DF=DN-BM;
(3)∵正方形的边长为16,DN=4,
∴CN=12.
根据(1)可知,BM+DN=MN,
设 MN=x,则 BM=x-4,
∴CM=16-(x-4)=20-x.
在Rt△CMN中,
∵MN2=CM2+CN2,
∴x2=(20-x)2+122.
解得 x=13.6.
∴MN=13.6cm.
点评:此题考查正方形的性质、全等三角形的判定和性质、勾股定理等知识点,运用截长补短法构造全等三角形是关键.也可运用图形的旋转性质构造全等三角形.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
