题目内容
一个三角形的两边分别为2和6，且第三边的长为奇数，则第三边可能为（ ）
分析：能够根据三角形的三边关系“任意两边之和＞第三边，任意两边之差＜第三边”，求得第三边的取值范围；再根据第三边是奇数，进行求解．
解答：解：根据三角形的三边关系，得：
6-2＜第三边长＜6+2，
即4＜第三边长＜8，
又∵第三边是奇数，
则第三边应是5或7．
故选：C．
6-2＜第三边长＜6+2，
即4＜第三边长＜8，
又∵第三边是奇数，
则第三边应是5或7．
故选：C．
点评：此题主要考查了三角形的三边关系，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．
练习册系列答案
课时训练江苏人民出版社系列答案
相关题目
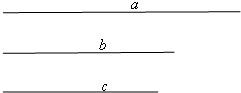
19、已知一个三角形的两边分别为a，b，这两边的夹角为α，请用尺规作图法作出这个三角形．