题目内容
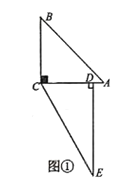
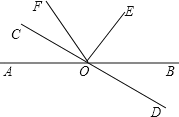
【题目】如图，直线
、
相交于
，∠EOC=90°，
是
的角平分线，
，求
的度数．其中一种解题过程如下：请在括号中注明根据，在横线上补全步骤．
解：∵
（ ）
∴
∵是的角平分线
∴
（ ）
∴
∵
（ ）
∴
（ ）
【答案】已知，56，∠EOF，角平分线的定义，22，∠EOB，平角的定义，22，同角的余角相等．
【解析】
利用角的和差得出∠EOF的度数，利用角平分线的定义得到∠AOF的度数，进而得到∠AOC的度数，根据平角的定义和余角的性质即可得出结论．
∵
( 已知 )
∴
56 
∵
是
的角平分线
∴
∠EOF 
( 角平分线的定义 )
∴
22
∵
∠EOB 
( 平角的定义 )
∴
22 ( 同角的余角相等 )．
故答案为：已知，56，∠EOF，角平分线的定义，22，∠EOB，平角的定义，22，同角的余角相等．
【题目】某市为了鼓励居民节约用水，采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过
时，按
计算，月用水量超过时，其中的仍按
元/
计算，超过部分按
元/
计算.设某户家庭月用水量
.
(1)用含
的式子表示:
当
时，水费为 元;当
时，水费为 元;
(2)
月份 | 4月 | 5月 | 6月 |
用水量 |
|
|
|
小花家第二季度用水情况如上表，小花家这个季度共缴纳水费
元，请你求出小花家
月份用水量
的值?
【题目】某校八年级两个班，各选派10名学生参加学校举行的“建模”大赛预赛，各参赛选手的成绩如下：
八（1）班：88，91，92，93，93，93，94，98，98，100；
八（2）班：89，93，93，93，95，96，96，98，98，99.
通过整理，得到数据分析表如下：
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
八（1）班 | 100 |
| 93 | 93 | 12 |
八（2）班 | 99 | 95 |
|
| 8.4 |
（1）直接写出表中
、
、
的值为：
_____，
_____，
_____；
（2）依据数据分析表，有人说：“最高分在（1）班，（1）班的成绩比（2）班好.”但也有人说（2）班的成绩要好.请给出两条支持八（2）班成绩好的理由；
（3）学校从平均数、中位数、众数、方差中选取确定了一个成绩，等于或大于这个成绩的学生被评定为“优秀”等级，如果八（2）班有一半的学生能够达到“优秀”等级，认为这个成绩应定为_____分.
