题目内容
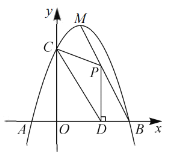
【题目】如图,抛物线y=a(x﹣![]() )(x+3)交x轴于点A、B,交y轴于点C,tan∠CAO=
)(x+3)交x轴于点A、B,交y轴于点C,tan∠CAO=![]() .
.
(1)求a值;
(2)点P为第一象限内抛物线上一点,点P的横坐标为t,连接PA,PC,设△PAC的面积为S,求S与t之间的关系式;
(3)在(2)的条件下,点Q在第一象限内的抛物线上(点Q在点P的上方),过点P作PE⊥AB,垂足为E,点D在线段AQ上,点F在线段AO上连接ED、DF,DE交AP于点G,若∠QDF+∠QDE=180°,∠DFA+∠AED=90°,PG=PE,PG:EF=3:2,求点P的坐标.

【答案】(1)a=﹣![]() ;(2)S=
;(2)S=![]() t2+
t2+![]() t;(3)点P(1,3)
t;(3)点P(1,3)
【解析】
(1)由题意可求点A,点B坐标,由锐角三角函数可求点C坐标,代入解析式可求解a的值;
(2)点P(t,﹣![]() t2﹣
t2﹣![]() t+4),由面积关系可求解;
t+4),由面积关系可求解;
(3)如图3,延长AQ,EP交于点H,连接GF,由四点共圆可证点A,点D,点G,点F四点共圆,可得∠ADF=∠AGF,∠QDE=∠AFG,设PG=PE=3a,EF=2a,由勾股定理可求a=![]() ,可求点P坐标,代入解析式可求解.
,可求点P坐标,代入解析式可求解.
解:(1)∵抛物线y=a(x﹣![]() )(x+3)交x轴于点A、B,
)(x+3)交x轴于点A、B,
∴0=a(x﹣![]() )(x+3)
)(x+3)
∴x1=![]() ,x2=﹣3,
,x2=﹣3,
∴点A(﹣3,0),点B(![]() ,0),
,0),
∴AO=3,
∵tan∠CAO=![]() =
=![]() ,
,
∴CO=4,
∴点C(0,4)
∴4=a(0﹣![]() )(0+3),
)(0+3),
∴a=﹣![]()
(2)∵y=﹣![]() (x﹣
(x﹣![]() )(x+3)
)(x+3)
∴y=﹣![]() x2﹣
x2﹣![]() x+4,
x+4,
∵点P的横坐标为t,
∴点P(t,﹣![]() t2﹣
t2﹣![]() t+4),
t+4),
∴S=![]() [4+(﹣
[4+(﹣![]() t2﹣
t2﹣![]() x+4)]t+
x+4)]t+![]() ×3×4﹣
×3×4﹣![]() ×(t+3)(﹣
×(t+3)(﹣![]() t2﹣
t2﹣![]() t+4)=
t+4)=![]() t2+
t2+![]() t;
t;
(3)如图3,延长AQ,EP交于点H,连接GF,
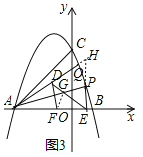
∵∠QDF+∠QDE=180°,且∠QDE+∠ADE=180°,
∴∠ADE=∠QDF,
∴∠ADF=∠QDE,
∵∠DFA+∠AED=90°,∠AED+∠DEP=90°,
∴∠AFD=∠DEP,
∴∠HAE=∠AHE,且HE⊥AE,
∴∠HAE=∠AHE=45°,
∴AE=EH=t+3,
∵PE=PG,
∴∠PGE=∠PEG,
∴∠PGE=∠AFD=∠AGD,
∴点A,点D,点G,点F四点共圆,
∴∠ADF=∠AGF,∠QDE=∠AFG,
∴∠AGF=∠AFG,
∴AF=AG,
设PG=PE=3a,EF=2a,
∴AF=t+3﹣2a=AG,AP=t+3﹣2a+3a=t+3+a,
∵AP2=PE2+AE2,
∴(t+3+a)2=9a2+(t+3)2,
∴a=![]() ,
,
∴3a=![]()
∴点P(t,![]() )
)
∴![]() =﹣
=﹣![]() t2﹣
t2﹣![]() t+4,
t+4,
∴t=1,t=﹣3(不合题意舍去)
∴点P(1,3)

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】如图,在![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,将线段
上的动点,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .若已知
.若已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() 两点间的距离为
两点间的距离为![]() 两点间的距离为
两点间的距离为![]() .(若同学们打印的BC的长度如不是
.(若同学们打印的BC的长度如不是![]() ,请同学们重新画图、测量)
,请同学们重新画图、测量)
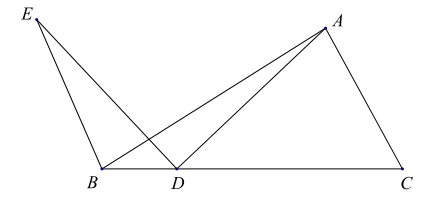
小明根据学习函数的经验,分别对![]() 自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整:
自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() 与
与![]() 的几组对应值,如下表:
的几组对应值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 7.03 | 6.20 | 5.44 | 4.76 | 4.21 | 3.85 | 3.73 | 3.87 | 4.26 |
|
| 5.66 | 4.32 |
| 1.97 | 1.59 | 2.27 | 3.43 | 4.73 |
写出![]() 的值.(保留1位小数)
的值.(保留1位小数)
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 的图象;
的图象;
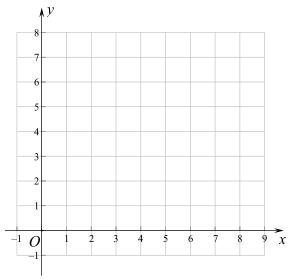
(3)结合函数图像,解决问题:
①当![]() 在线段
在线段![]() 上时,
上时,![]() 的长度约为________
的长度约为________![]() ;
;
②当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度
的长度![]() 约为_______
约为_______![]() .
.