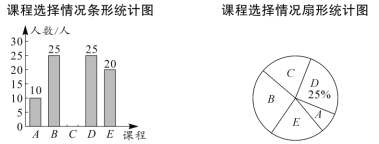
题目内容
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点(点
两点(点![]() 位于点
位于点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() ,
,![]() 是抛物线的顶点,直线
是抛物线的顶点,直线![]() 是抛物线的对称轴,且点
是抛物线的对称轴,且点![]() 的坐标为
的坐标为![]() .
.
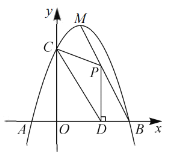
(1)求抛物线的解析式.
(2)已知![]() 为线段
为线段![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() .若
.若![]() 的面积为
的面积为![]() .
.
①求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 取得最值时,求点
取得最值时,求点![]() 的坐标.
的坐标.
(3)在(2)的条件下,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形?如果存在,请求出点
为等腰三角形?如果存在,请求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②当
;②当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,此时
,此时![]() ;(3)存在,点
;(3)存在,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)点C坐标代入解析式可求c的值,由对称轴可求b的值,即可求解;
(2)①先求出点M,点A,点B的坐标,利用待定系数法可求BM解析式,由三角形的面积公式可求解;
②利用二次函数的性质可求解;
(3)分三种情况讨论,利用两点距离公式列出方程可求解.
(1)![]() 抛物线
抛物线![]() 的对称轴为直线
的对称轴为直线![]() .
.
又![]() 抛物线与
抛物线与![]() 轴的交点为
轴的交点为![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
(2)①![]() 顶点
顶点![]() .
.
设直线![]() 的解析式为
的解析式为![]() .
.
将![]() 代入,
代入,
得![]() 解得
解得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
![]() 轴且
轴且![]() ,
,
![]() 的面积
的面积![]() .
.
![]() 点
点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,
![]() ,
,
故![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() .
.
②![]() ,
,
![]() 当
当![]() 时,
时,![]() 取得最大值
取得最大值![]() ;
;
当![]() 时,
时,![]() 没有最小值.
没有最小值.
综上,当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,此时
,此时![]()
(3)存在.
当![]() 时,
时,
![]() ,
,
![]() ,
,
解得![]() (舍去)或
(舍去)或![]() ,此时
,此时![]() .
.
当![]() 时,
时,
![]()
![]()
解得![]() (舍去)或
(舍去)或![]() ,此时
,此时![]() .
.
当![]() 时,
时,
![]() ,
,
![]() ,
,
解得![]() 或
或![]() ,均不符合题意,舍去.
,均不符合题意,舍去.
综上所诉,存在点![]() 使
使![]() 为等腰三角形,点
为等腰三角形,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案【题目】为了坚持以人民为中心的发展思想,以不断改善民生为发展的根本目的,某机构随机对某小区部分居民进行了关于“社区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表,根据图标信息,解答下列问题:
满意度 | 人数 | 所占百分比 |
非常满意 | 12 |
|
满意 | 54 |
|
比较满意 |
|
|
不满意 | 6 |
|
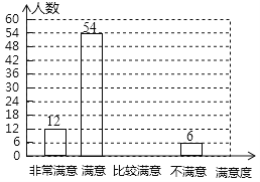
(1)本次调查的总人数为_______.
(2)请补全条形统计图;
(3)据统计,该社区服务站平均每天接待居民约1000名,若将“非常满意”和“消意”作为居民对社区服务站服务工作的肯定,请你估计该社区服务站服务工作平均每天得到多少名居民的肯定.