题目内容
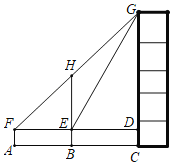
【题目】如图,在ABCD中,∠ABD=90°,AD= 5,BD=3,点P从点A出发,沿折线AB- BC以每秒个单位长度的速度向终点C运动(点P不与点A、B、C重合).在点P运动的过程中,过点P作AB所在直线的垂线.交边AD或边CD于点Q,以PQ为一边作矩形PQMN,且QM=2.MN与BD在PQ的同侧,设点P的运动时间为t(秒),
(1)当t= 5时,求线段CP的长;
(2)求线段PQ的长(用含t的代数式表示);
(3)当点M落在BD上时,求t的值;
(4)当矩形PQMN与ABCD重叠部分圆形为五边形时,直接写出t的取值范围.
【答案】(1)4;(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(3)2或
;(3)2或![]() ;(4)
;(4)![]() ,
,![]()
【解析】
(1)如图1中,利用勾股定理求出AB的长,t=5时,点P在线段BC上,易知PB=1,PC=4;
(2)分两种情形求解即可①如图2中,当0<t<4时,②如图3中,当5<t<10时;
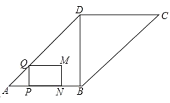
(3)分两种情形求解即可①如图4中,当点P在线段AB上时,点M在线段BD上,求出AP.②如图5中,当点P在线段BC上,点M与D重合时;
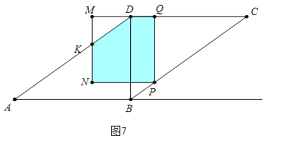
(4)分两种情形分别求解即可①如图6中,当点P在线段AB上,重叠部分是五边形PBKMQ时,2<t<4.②如图7中,当点P在线段BC上,重叠部分是五边形PQDKN时,4<t<6.5;
(1)如图1中,
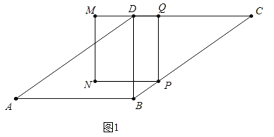
在Rt△ABD中,∵∠ABD=90![]() ,AD=5,BD=3,
,AD=5,BD=3,
∴AB=![]() =4,
=4,
∵四边形ABCD是平行四边形,
∴AD=BC=5,CD=AB=4,
当t=5时,点P在BC上,PB=1,
∴PC=4.
(2)①如图2中,当0<t<4时,
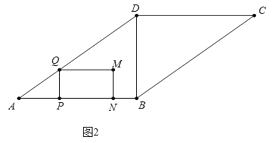
∵PQ∥BD,
∴![]() ,
,
∴![]() ,
,
∴PQ=![]() t.
t.
②如图3中,当5<t<10时,
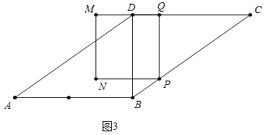
∵PQ∥BD,
∴![]() ,
,
∴![]() ,
,
∴PQ=![]() (9t).
(9t).
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
(3)①如图4中,当点P在线段AB上时,点M在线段BD上,
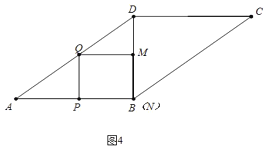
∵QM∥AB,
∴![]() ,
,
∴![]() ,
,
∴DQ=![]() ,
,
∴AQ=DQ,
∵PQ∥BD,
∴AP=PB=2,
∴t=2.
②如图5中,当点P在线段BC上,点M与D重合时,
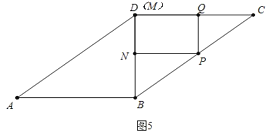
∵QM=2,∴CQ=CD- QM=2,
∴Q点是CD中点,
故PQ是△BCD是中位线
故PB=PC=![]() BC=
BC=![]() ,
,
此时t=4+![]() =
=![]() .
.
∴当点M落在BD上时,求t的值为2或![]() ;
;
(4)①如图6中,重叠部分是五边形PBKMQ
由图4可知,当P点为AB中点时,t=2
当P点与B点重合时,t=4
故当点P在线段AB上,重叠部分是五边形PBKMQ时,2<t<4;
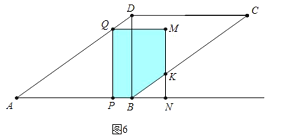
②如图7中,重叠部分是五边形PQDKN,
由图5可知,当P点为BC中点时,t=![]() ,
,
当P点与B点重合时,t=4,
当点P在线段BC上,重叠部分是五边形PQDKN时,4<t<6.5.
∴当矩形POMN与ABCD重叠部分圆形为五边形时, t的取值范围是2<t<4或4<t<6.5.