题目内容
1.如图1,正△ABC和Rt△ABD中,∠ADB=90°.(1)如图2,在四边形ADBC中以AD为边作等边△ADE,求证:CE=BD;
(2)如图3,在(1)的条件下,延长CE交DB于F,求证:DF=EF;
(3)若BC=6,△ABD的内切圆的半径为r,则r的最大值为3$\sqrt{2}$-3(直接写出答案)

分析 (1)欲证明CE=BD,只要证明△ADB≌△AEC即可.
(2)由△DAB≌△EAC,推出∠AEC=∠ADB=∠AEF=90°,由∠ADE=∠AED=60°,推出∠FDE=∠FED=30°,即可证明.
(3)设BD=m,AD=n,则r=$\frac{m+n-6}{2}$=$\frac{m+n}{2}$-3,由m2+n2=36,因为36=m2+n2≥$\frac{(m+n)^{2}}{2}$,推出m+n≤6$\sqrt{2}$,由此即可解决问题.
解答 (1)证明:如图2中,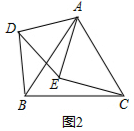
∵△ADE是等边三角形,△ABC是等边三角形
∴AD=AE,AB=AC,∠DAE=∠BAC=60°,
∴∠DAB=∠EAC,
在△ADB和△AEC中,
$\left\{\begin{array}{l}{AD=AE}\\{∠BAD=∠CAE}\\{AB=AC}\end{array}\right.$,
∴△ADB≌△AEC,
∴BD=CE.
(2)证明:如图3中,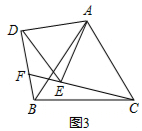
由(1)可知,△DAB≌△EAC,
∴∠AEC=∠ADB=∠AEF=90°,
∵∠ADE=∠AED=60°,
∴∠FDE=∠FED=30°,
∴FD=FE,
(3)解:设BD=m,AD=n,则r=$\frac{m+n-6}{2}$=$\frac{m+n}{2}$-3,
∵m2+n2=36,
∵36=m2+n2≥$\frac{(m+n)^{2}}{2}$,
∴m+n≤6$\sqrt{2}$,
∴r≤3$\sqrt{2}$-3,
∴r的最大值为3$\sqrt{2}$-3.
故答案为3$\sqrt{2}$-3.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质、不等式的性质等知识,解题的关键是正确寻找全等三角形,难点是理解不等式的性质m2+n2≥$\frac{(m+n)^{2}}{2}$的应用,属于中考压轴题

 中考解读考点精练系列答案
中考解读考点精练系列答案| A. | 2 | B. | 0 | C. | -5 | D. | 4 |
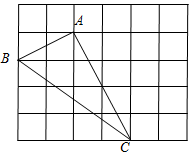 如图正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识求△ABC的面积.
如图正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识求△ABC的面积.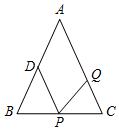 如图,等腰△ABC中,∠B=∠C,AB=AC=20cm,BC=16cm,点D为AB中点,如果点P在线段BC上以2cm/s 的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.当△BPD与△CQP全等时,点Q的运动速度为2或$\frac{5}{2}$cm/s.
如图,等腰△ABC中,∠B=∠C,AB=AC=20cm,BC=16cm,点D为AB中点,如果点P在线段BC上以2cm/s 的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.当△BPD与△CQP全等时,点Q的运动速度为2或$\frac{5}{2}$cm/s.