题目内容
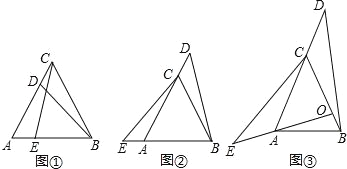
【题目】感知:如图①,在等边三角形ABC中,点D、E分别在边AC、AB上,若AE=CD,易知△ACE≌△CBD.
探究:若图①中的点D、E分别在边AC、BA的延长线上时,如图②,△ACE与△CBD是否仍然全等?如果全等,请证明:如果不全等,请说明理由.
应用:若图②中的等边三角形ABC为等腰三角形,且AC=BC,点O是AC边的垂直平分线与BC的交点,点D、E分别在AC、OA的延长线上,如图③,若AE=CD,∠ACB=α,∠ADB=β,则∠ACE的大小为 (用含α和β的代数式表示).
【答案】感知:证明见解析;探究:证明见解析;应用:α-β.
【解析】
试题分析:感知:由△ABC是等边三角形,可得AC=CB,∠ACE=∠B=60°,又由BD=CE,即可证得△ACE≌△CBD;
探究:根据△ABC是等边三角形,得到AC=CB,∠A=∠ACB=60°,由SAS证明△ACE≌△CBD.
应用:证明△ACE≌△CBD,得到∠AEC=∠CDB=β,根据外角的性质得到∠CAB=∠ACE+∠AEC,即可解答.
试题解析:感知:∵△ABC是等边三角形,
∴AC=CB,∠CAE=∠B=60°,
在△ACE和△CBD中,
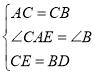
∴△ACE≌△CBD(SAS).
探究:△ACE与△CBD是否仍然全等,
∵△ABC是等边三角形,
∴AC=CB,∠A=∠ACB=60°,
∴∠EAC=∠DCB,
在△ACE和△CBD中,
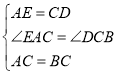
∴△ACE≌△CBD.
应用:∵点O是AC边的垂直平分线与BC的交点,
∴CO=AO,
∴∠ACB=∠CAO=α,
∵∠ACB+∠BCD=180°,∠EAC+∠CAO=180°,
∴∠EAC=∠DCB,
∵△ABC为等边三角形,
∴AC=BC,
在△EAC和△DCB中,
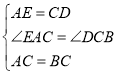
∴△EAC≌△DCB,
∴∠AEC=∠CDB=β,
∵∠CAB=∠ACE+∠AEC,
∴∠ACE=∠CAB-∠AEC=α-β.

 阅读快车系列答案
阅读快车系列答案