题目内容
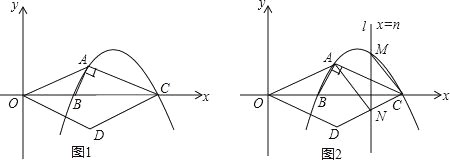
【题目】如图1，抛物线y=ax2-11ax+24a（a＜0）与x轴交于B、C两点（点B在点C的左侧），抛物线上另有一点A在第一象限内，且∠BAC=90°．
（1）求线段OC的长和点B的坐标；
（2）连接OA，将△OAC沿x轴翻折后得△ODC，当四边形OACD是菱形时，求此时抛物线的解析式；
（3）如图2，折垂直于x轴的直线l：x=n与（2）中所求的抛物线交于点M，与CD交于点N，若直线l沿x轴方向左右平移，且交点M始终位于抛物线上A、C两点之间时，试探究：当n为何值时，四边形AMCN的面积取得最大值，并求这个最大值；
（4）在（3）的条件下，当取得最大值时，四边形ADNM是否为平行四边形？直接回答 （是或不是）．如果不是，请直接写出此时的点M的坐标．
【答案】（1）OC=8，B点坐标为（3，0）；（2）抛物线的解析式为y=-
x2+
x-12；（3）最大值为9；（4）不，M点的坐标为（5，3）.
【解析】
试题分析：（1）根据二次函数与x轴交点坐标求法，解一元二次方程即可得出；
（2）利用菱形性质得出AD⊥OC，进而得出△ACE∽△BAE，即可得出A点坐标，进而求出二次函数解析式；
（3）首先求出过C、D两点的坐标的直线CD的解析式，进而利用S四边形AMCN=S△AMN+S△CMN求出即可；
（4）由条件可求得AD和MN，此时AD≠MN，可判定四边形ADNM不是平行四边形，由（3）容易求得M的坐标．
试题解析：（1）∵抛物线y=ax2-11ax+24a （a＜0）与x轴交于B、C两点（点B在点C的左侧），
∴令y=0可得0=ax2-11ax+24a，解得x1=3，x2=8，
∴OC=8，B点坐标为（3，0）；
（2）如图1，连接AD，交OC于点E，
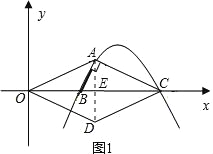
∵四边形OACD是菱形，
∴AD⊥OC，OE=EC=
OC=×8=4，
∴BE=4-3=1，
又∵∠BAC=90°，
∴△ACE∽△BAE，
∴
，
∴AE2=BECE=1×4，
∴AE=2，
∴点A的坐标为（4，2），
把点A的坐标（4，2）代入抛物线y=ax2-11ax+24a，得a=-，
∴抛物线的解析式为y=-x2+
x-12；
（3）如图2，连接AD，交OC于点E，
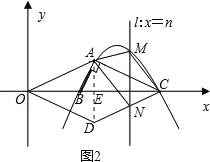
∵直线x=n与抛物线交于点M，
∴点M的坐标为（n，-n2+
n-12），
由（2）知，点D的坐标为（4，-2），
设直线CD的解析式为y=kx+b，
把C、D两点坐标代入可得
，解得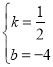
，
∴直线CD的解析式为y=x-4，
∴点N的坐标为（n，n-4），
∴MN=（-n2+
n-12）-（n-4）=-
n2+5n-8，
∴S四边形AMCN=S△AMN+S△CMN=MNCE=（-n2+5n-8）×4=-（n-5）2+9，
∴当n=5时，四边形AMCN的面积有最大值，最大值为9；
（4）由（3）可知n=5，且MN=9，
∵A（4，2），D（4，-2），
∴AD=4≠MN，
∴四边形ADNM不是平行四边形，
当n=5时，代入y=-n2+
n-12可求得y=3，
∴此时M点的坐标为（5，3）.
