题目内容
 (2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为
(2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为2
| ||
| π |
2
| ||
| π |
分析:若两个阴影部分的面积相等,那么△ABC和扇形ADF的面积就相等,可分别表示出两者的面积,然后列出方程即可求出AF的长度.
解答: 解:∵图中两个阴影部分的面积相等,
解:∵图中两个阴影部分的面积相等,
∴S扇形ADF=S△ABC,即:
=
×AC×BC,
又∵AC=BC=1,
∴AF2=
,
∴AF=
.
故答案为
.
 解:∵图中两个阴影部分的面积相等,
解:∵图中两个阴影部分的面积相等,∴S扇形ADF=S△ABC,即:
| 45π×AF2 |
| 360 |
| 1 |
| 2 |
又∵AC=BC=1,
∴AF2=
| 4 |
| π |
∴AF=
2
| ||
| π |
故答案为
2
| ||
| π |
点评:此题主要考查了扇形面积的计算方法及等腰直角三角形的性质,能够根据题意得到△ABC和扇形ADF的面积相等,是解决此题的关键,难度一般.

练习册系列答案
相关题目
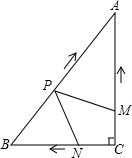 (2013•遵义)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).
(2013•遵义)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).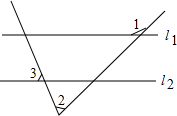 (2013•遵义)如图,直线l1∥l2,若∠1=140°,∠2=70°,则∠3的度数是( )
(2013•遵义)如图,直线l1∥l2,若∠1=140°,∠2=70°,则∠3的度数是( )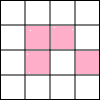 (2013•遵义)如图,在4×4正方形网格中,任选取一个白色的小正方形并涂红,使图中红色部分的图形构成一个轴对称图形的概率是( )
(2013•遵义)如图,在4×4正方形网格中,任选取一个白色的小正方形并涂红,使图中红色部分的图形构成一个轴对称图形的概率是( )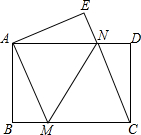 (2013•遵义)如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(2013•遵义)如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N. (2013•遵义)如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-
(2013•遵义)如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-