题目内容
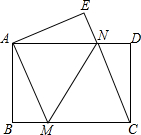 (2013•遵义)如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(2013•遵义)如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3:1,求
| MN | DN |
分析:(1)由折叠的性质可得:∠ANM=∠CNM,由四边形ABCD是矩形,可得∠ANM=∠CMN,则可证得∠CMN=∠CNM,继而可得CM=CN;
(2)首先过点N作NH⊥BC于点H,由△CMN的面积与△CDN的面积比为3:1,易得MC=3ND=3HC,然后设DN=x,由勾股定理,可求得MN的长,继而求得答案.
(2)首先过点N作NH⊥BC于点H,由△CMN的面积与△CDN的面积比为3:1,易得MC=3ND=3HC,然后设DN=x,由勾股定理,可求得MN的长,继而求得答案.
解答:(1)证明:由折叠的性质可得:∠ANM=∠CNM,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ANM=∠CMN,
∴∠CMN=∠CNM,
∴CM=CN;

(2)解:过点N作NH⊥BC于点H,
则四边形NHCD是矩形,
∴HC=DN,NH=DC,
∵△CMN的面积与△CDN的面积比为3:1,
∴
=
=
=3,
∴MC=3ND=3HC,
∴MH=2HC,
设DN=x,则HC=x,MH=2x,
∴CM=3x=CN,
在Rt△CDN中,DC=
=2
x,
∴HN=2
x,
在Rt△MNH中,MN=
=2
x,
∴
=
=2
.
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ANM=∠CMN,
∴∠CMN=∠CNM,
∴CM=CN;

(2)解:过点N作NH⊥BC于点H,
则四边形NHCD是矩形,
∴HC=DN,NH=DC,
∵△CMN的面积与△CDN的面积比为3:1,
∴
| S△CMN |
| S△CDN |
| ||
|
| MC |
| ND |
∴MC=3ND=3HC,
∴MH=2HC,
设DN=x,则HC=x,MH=2x,
∴CM=3x=CN,
在Rt△CDN中,DC=
| CN2-DN2 |
| 2 |
∴HN=2
| 2 |
在Rt△MNH中,MN=
| MH2+HN2 |
| 3 |
∴
| MN |
| DN |
2
| ||
| x |
| 3 |
点评:此题考查了矩形的性质、折叠的性质、勾股定理以及三角形的面积.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
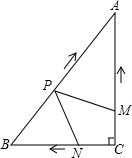 (2013•遵义)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).
(2013•遵义)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).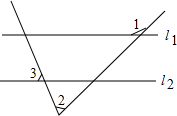 (2013•遵义)如图,直线l1∥l2,若∠1=140°,∠2=70°,则∠3的度数是( )
(2013•遵义)如图,直线l1∥l2,若∠1=140°,∠2=70°,则∠3的度数是( )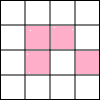 (2013•遵义)如图,在4×4正方形网格中,任选取一个白色的小正方形并涂红,使图中红色部分的图形构成一个轴对称图形的概率是( )
(2013•遵义)如图,在4×4正方形网格中,任选取一个白色的小正方形并涂红,使图中红色部分的图形构成一个轴对称图形的概率是( )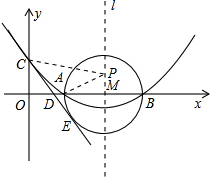 (2013•遵义)如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-
(2013•遵义)如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-