题目内容
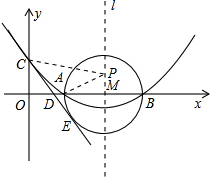 (2013•遵义)如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-
(2013•遵义)如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-| 2 | 3 |
(1)求抛物线的解析式及A,B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
分析:(1)利用顶点式求得二次函数的解析式后令其等于0后求得x的值即为与x轴交点坐标的横坐标;
(2)线段BC的长即为AP+CP的最小值;
(3)连接ME,根据CE是⊙M的切线得到ME⊥CE,∠CEM=90°,从而证得△COD≌△MED,设OD=x,在RT△COD中,利用勾股定理求得x的值即可求得点D的坐标,然后利用待定系数法确定线段CE的解析式即可.
(2)线段BC的长即为AP+CP的最小值;
(3)连接ME,根据CE是⊙M的切线得到ME⊥CE,∠CEM=90°,从而证得△COD≌△MED,设OD=x,在RT△COD中,利用勾股定理求得x的值即可求得点D的坐标,然后利用待定系数法确定线段CE的解析式即可.
解答: 解:(1)由题意,设抛物线的解析式为y=a(x-4)2-
解:(1)由题意,设抛物线的解析式为y=a(x-4)2-
(a≠0)
∵抛物线经过(0,2)
∴a(0-4)2-
=2
解得:a=
∴y=
(x-4)2-
即:y=
x2-
x+2
当y=0时,
x2-
x+2=0
解得:x=2或x=6
∴A(2,0),B(6,0);
(2)存在,
如图2,由(1)知:抛物线的对称轴l为x=4,
因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,所以AP+CP=BC的值最小
∵B(6,0),C(0,2)
∴OB=6,OC=2
∴BC=2
,
∴AP+CP=BC=2
∴AP+CP的最小值为2
;
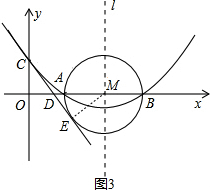
(3)如图3,连接ME
∵CE是⊙M的切线
∴ME⊥CE,∠CEM=90°
由题意,得OC=ME=2,∠ODC=∠MDE
∵在△COD与△MED中
∴△COD≌△MED(AAS),
∴OD=DE,DC=DM
设OD=x
 则CD=DM=OM-OD=4-x
则CD=DM=OM-OD=4-x
则RT△COD中,OD2+OC2=CD2,
∴x2+22=(4-x)2
∴x=
∴D(
,0)
设直线CE的解析式为y=kx+b(k≠0),
∵直线CE过C(0,2),D(
,0)两点,
则
解得:
∴直线CE的解析式为y=-
x+2;
 解:(1)由题意,设抛物线的解析式为y=a(x-4)2-
解:(1)由题意,设抛物线的解析式为y=a(x-4)2-| 2 |
| 3 |
∵抛物线经过(0,2)
∴a(0-4)2-
| 2 |
| 3 |
解得:a=
| 1 |
| 6 |
∴y=
| 1 |
| 6 |
| 2 |
| 3 |
即:y=
| 1 |
| 6 |
| 4 |
| 3 |
当y=0时,
| 1 |
| 6 |
| 4 |
| 3 |
解得:x=2或x=6
∴A(2,0),B(6,0);
(2)存在,
如图2,由(1)知:抛物线的对称轴l为x=4,
因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,所以AP+CP=BC的值最小
∵B(6,0),C(0,2)
∴OB=6,OC=2
∴BC=2
| 10 |

∴AP+CP=BC=2
| 10 |
∴AP+CP的最小值为2
| 10 |
(3)如图3,连接ME
∵CE是⊙M的切线
∴ME⊥CE,∠CEM=90°
由题意,得OC=ME=2,∠ODC=∠MDE
∵在△COD与△MED中
|
∴△COD≌△MED(AAS),
∴OD=DE,DC=DM
设OD=x
 则CD=DM=OM-OD=4-x
则CD=DM=OM-OD=4-x则RT△COD中,OD2+OC2=CD2,
∴x2+22=(4-x)2
∴x=
| 3 |
| 2 |
∴D(
| 3 |
| 2 |
设直线CE的解析式为y=kx+b(k≠0),
∵直线CE过C(0,2),D(
| 3 |
| 2 |
则
|
解得:
|
∴直线CE的解析式为y=-
| 4 |
| 3 |
点评:本题考查了二次函数的综合知识,特别是用顶点式求二次函数的解析式,更是中考中的常考内容,本题难度偏大.

练习册系列答案
相关题目
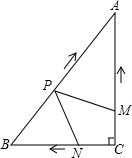 (2013•遵义)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).
(2013•遵义)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).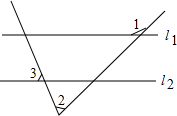 (2013•遵义)如图,直线l1∥l2,若∠1=140°,∠2=70°,则∠3的度数是( )
(2013•遵义)如图,直线l1∥l2,若∠1=140°,∠2=70°,则∠3的度数是( )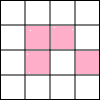 (2013•遵义)如图,在4×4正方形网格中,任选取一个白色的小正方形并涂红,使图中红色部分的图形构成一个轴对称图形的概率是( )
(2013•遵义)如图,在4×4正方形网格中,任选取一个白色的小正方形并涂红,使图中红色部分的图形构成一个轴对称图形的概率是( )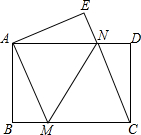 (2013•遵义)如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(2013•遵义)如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.