题目内容
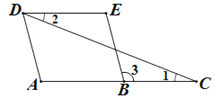
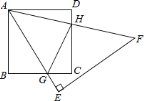
【题目】如图,正方形ABCD的面积为1cm2,△AEF为等腰直角三角形,∠E=90°,AE和BC交于点G,AF和CD交于点H,则△CGH的周长_________
【答案】2
【解析】
延长CB至M,使BM=DH,连接AM;先证明△ABM≌△ADH(SAS),得出AM=AH,∠BAM=∠DAH,证出∠MAG=∠HAG,再证明△AMB≌△AHG(SAS)得出GM=GH,即可求出结果.
延长CB至M,使BM=DH,连接AM;如图所示:
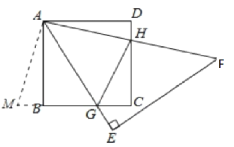
∵四边形ABCD是正方形,正方形ABCD的面积为1cm![]() ,
,
∴AB=BC=CD=1,∠BAD=∠ABC=∠D=90°,
∴∠ABM=90°,
在△ABM和△ADH中,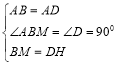 ,
,
∴△ABM≌△ADH(SAS),
∴AM=AH,∠BAM=∠DAH,
∵△AEF是等腰直角三角形,
∴∠HAG=45°,
∴∠BAG+∠DAH=45°,
∴∠MAG=45°,
在△AMG和△AHG中,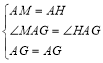 ,
,
∴△AMG≌△AHG(SAS),
∴GM=GH,
∴△CGH的周长=GH+CG+CH=GM+CG+CH
=BM+BG+CG+CH=DH+BG+CG+CH=BC+CD=2
故答案为:2

练习册系列答案
相关题目