��Ŀ����
����Ŀ����֪ʶ���ɣ�
�����Ѿ�֪����ͨ����ͬ�ķ�����ʾͬһͼ�ε����������̽����Ӧ�ĵ�ʽ��
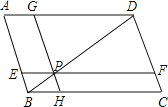
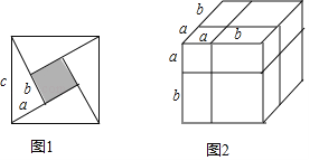
2002��8���ڱ����ٿ��˹�����ѧ��ᣬ�������ͼ1��ʾ���������ĸ���״��С��ȫ��ͬ��ֱ�����������м��С������ƴ�ɵ�һ���������Σ�ֱ�������ε�����ֱ�DZ߳��ֱ�Ϊa��b �� a<b ����б�߳�Ϊc��
��1��ͼ����Ӱ���ֵ���������ַ����ɷֱ��ʾΪ�� �� ���� �� ��
��2�����ܵó���a��b��c֮���������ϵ���� �� ���Ⱥ������軯Ϊ�����ʽ����
��3��һֱ�������ε�����ֱ�DZ߳�Ϊ6��8������б�߳�Ϊ�� �� ��
��֪ʶǨ�ƣ�
ͨ����ͬ�ķ�����ʾͬһ������������Ҳ����̽����Ӧ�ĵ�ʽ����ͼ2�DZ߳�Ϊa+b�������壬����ͼ��ʾ�ķָ��߷ֳ�8�飮
��4���ò�ͬ�����������������������Ϳ��Եõ�һ����ʽ�������ʽ����Ϊ�� �� �����Ⱥ������軯Ϊ�����ʽ��
��5����֪a+b��3��ab��1����������Ĺ�����a3+b3��ֵ��
���𰸡���1��c2��2ab����b��a��2����2��a2+b2��c2����3��10����4����a+b��3��a3+b3+3a2b+3ab2����5��a3+b3��18��
��������
��1�����ͼ�εĸ������ֵ���������ɵó��𰸣�
��2�����ݣ�1���Ľ�������ɵó��𰸣�
��3������������ɣ�
��4�������������������������ֵ���������ɵó��𰸣�
��5�����루4���еĵ�ʽ������ɣ�
�⣺
��1������c2��2ab����b��a��2��
��2������a2+b2��c2��
��3������10��
��4��ͼ�ε����Ϊ��a+b��3��a3+b3+a2b+a2b+a2b+ab2+ab2+ab2��
����a+b��3��a3+b3+3a2b+3ab2��
�ʴ�Ϊ����a+b��3��a3+b3+3a2b+3ab2��
��5����a+b��3��ab��1����a+b��3��a3+b3+3a2b+3ab2����a3+b3+3ab��a+b��
��33��a3+b3+3��1��3��
��ã�a3+b3��18��