��Ŀ����
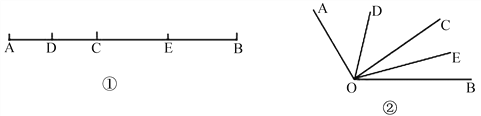
����Ŀ����ͼ������AOB��90�㣬��AOCΪ��AOB���һ���ǣ��ҡ�AOC��30�㣬����OMƽ�֡�BOC��ONƽ�֡�AOC��
��1�����MON�Ķ�����
��2�������1���С�AOB��������AOC��������������Ϊ��ǣ��������������䣬�����MON�Ķ�����
��3����ʵ�߶εļ�����ǵļ�������Ž��ܵ���ϵ����ͼ���߶�AB��m���ӳ��߶�AB��C��ʹ��BC��n����M��N�ֱ�ΪAC��BC���е㣬��MN�ij���ֱ��д���������
���𰸡���1��45�㣻��2��![]() ����3��MN��
����3��MN��![]() m��
m��
��������
��1�����ݽǵ�ƽ���ߵ��ص㣬���Ե�֪����������ȣ�����ԭ�ǵ�һ�룬���ݽ����֮���������ϵ���ɵó����ۣ�
��2�����ݽǵ�ƽ���ߵ��ص㣬���Ե�֪����������ȣ�����ԭ�ǵ�һ�룬���ݽ����֮���������ϵ���ɵó����ۣ�
��3�����ݣ�2����ԭ������ֱ�ӵó����ۣ�
�⣺��1���ߡ�BOC����AOB+��AOC��90��+30�㣽120�㣬
����OMƽ�֡�BOC��
���COM��![]() ��BOC��
��BOC��![]() ��120�㣽60�㣬
��120�㣽60�㣬
��ONƽ�֡�AOC��
���CON��![]() ��AOC��
��AOC��![]() ��30�㣽15�㣬
��30�㣽15�㣬
���MON����COM����CON��60�㩁15�㣽45�㣮
��2���ߡ�BOC����AOB+��AOC����+����
������OMƽ�֡�BOC��
���COM��![]() ��BOC��
��BOC��![]() ����+������
����+������
��ONƽ�֡�AOC��
���CON��![]() ��AOC��
��AOC��![]() ����
����
���MON����COM����CON��![]() ����+������
����+������![]() ����
����![]() ����
����
��3��MN��![]() m��
m��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij�������е�һ����6000Ԫ�����ס���������Ʒ����������Ʒ�ļ����ȼ���Ʒ������![]() ����15�����ס���������Ʒ�Ľ��ۺ��ۼ����±�����ע���������ۼ۩����ۣ�
����15�����ס���������Ʒ�Ľ��ۺ��ۼ����±�����ע���������ۼ۩����ۣ�
�� | �� | |
���ۣ�Ԫ/���� | 22 | 30 |
�ۼۣ�Ԫ/���� | 29 | 40 |
��1���ó��й����ס���������Ʒ�����ټ���
��2���ó��н���һ�ι����ļס���������Ʒȫ�������һ���ɻ�ö�������
��3���ó��еڶ����Ե�һ�εĽ����ֹ����ס���������Ʒ�����м���Ʒ�ļ������䣬����Ʒ�ļ����ǵ�һ�ε�3��������Ʒ��ԭ�����ۣ�����Ʒ�������ۣ��ڶ���������Ʒ���������Ժ��õ�������ȵ�һ�λ�õ��������180Ԫ����ڶ�������Ʒ�ǰ�ԭ�۴������ۣ�