题目内容
如图,DE是△ABC边AB的垂直平分线,分别交AB、BC于D、E。AE平分∠BAC. 设∠B = x(单位:度),∠C = y(单位:度).

(1)求y随x变化的函数关系式,并写出自变量x的取值范围;
(2)请讨论当△ABC为等腰三角形时,∠B为多少度?

(1)求y随x变化的函数关系式,并写出自变量x的取值范围;
(2)请讨论当△ABC为等腰三角形时,∠B为多少度?
(1)y =" 180" – 3x,0< x <60(2)45º或36º
解:(1)∵DE 垂直平分AB,∴∠BAE = ∠B =x,
又∵AE平分∠BAC,∴∠BAC =2∠BAE = 2x---------------------1/
∴ y =" 180" – 3x ------------------------------------------2/
0< x <60-----------------------------------------------3/
(2)显然,AC≠BC-----------------------------------------4/.
若 AB = AC,此时,x = y,即:180-3x = x--------------5/
得:x = 45(度);------------------------------------6/
若 AB = BC,此时,2x = y,即:180 – 3x = 2x
得:x = 36(度).
∴当△ABC为等腰三角形时,∠B分别为45º或36º----------------8/
(1)根据线段的垂直平分线求出∠BAE的度数,求出∠BAC即可;
(2)AB=AC时,得出180-3x=x,求出即可;AB=BC时,得出180-3x=2x,求出即可.
又∵AE平分∠BAC,∴∠BAC =2∠BAE = 2x---------------------1/
∴ y =" 180" – 3x ------------------------------------------2/
0< x <60-----------------------------------------------3/
(2)显然,AC≠BC-----------------------------------------4/.
若 AB = AC,此时,x = y,即:180-3x = x--------------5/
得:x = 45(度);------------------------------------6/
若 AB = BC,此时,2x = y,即:180 – 3x = 2x
得:x = 36(度).
∴当△ABC为等腰三角形时,∠B分别为45º或36º----------------8/
(1)根据线段的垂直平分线求出∠BAE的度数,求出∠BAC即可;
(2)AB=AC时,得出180-3x=x,求出即可;AB=BC时,得出180-3x=2x,求出即可.

练习册系列答案
相关题目
 (千米)的一次函数.南通气象台某仪器显示,某时刻高出地面2千米处温度为8℃,高出地面5千米处温度为零下10℃.
(千米)的一次函数.南通气象台某仪器显示,某时刻高出地面2千米处温度为8℃,高出地面5千米处温度为零下10℃. 与
与
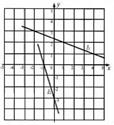
 (米)与注水时间
(米)与注水时间 (小时)之间的关系如图所示,根据图像提供的信息,回答下列问题:
(小时)之间的关系如图所示,根据图像提供的信息,回答下列问题:
 (单位:百万平方米),与时间
(单位:百万平方米),与时间 的关系是
的关系是 ,(
,( 且
且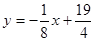 (
(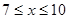 且
且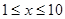 且
且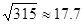 ,
, ,
,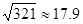 )
)