题目内容
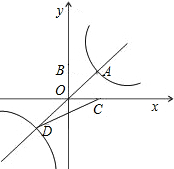 如图,正比例函数y=k1x与反比例函数y=
如图,正比例函数y=k1x与反比例函数y=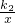 的图象交于点A,从点A向x轴和y轴分别作垂线,所组成的正方形的面积为4.
的图象交于点A,从点A向x轴和y轴分别作垂线,所组成的正方形的面积为4.
(1)分别求出正比例函数和反比例函数的函数关系式.
(2)若正比例函数与反比例函数的另一交点D的坐标为(-2,n),求n的值.
(3)求△ODC的面积.
解
(1)∵正方形ABOC的面积为4,
∴|k2|=4,
而A点的横纵坐标相等,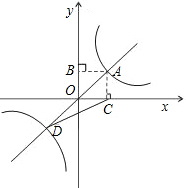
∴|k2|=4,
即A(2,2),
∴2=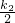 ,
,
即k2=4,
∴反比例函数解析式为y= .
.
把A(2,2)代入y=k1x中,
∴2=2k1,
∴k1=1,
∴正比例函数的解析式为y=x;
(2)把x=-2代入y=x,得y=-2,
∴n=-2;
(3)根据(2)得D(-2,-2),
∵c(2,0),
∴S△ODC= ×2×2=2.
×2×2=2.
分析:(1)根据正方形的面积为4,易求A点坐标,分别代入函数表达式求解;
(2)把x=-2代入任一解析式可求纵坐标n;
(3)由D点坐标即可求△ODC的面积.
点评:此题要求学生熟练掌握利用待定系数法求函数解析式,同时会利用反比例函数图象和性质解决问题,解题时注意点的坐标与线段长度的联系.
(1)∵正方形ABOC的面积为4,
∴|k2|=4,
而A点的横纵坐标相等,

∴|k2|=4,
即A(2,2),
∴2=
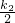 ,
,即k2=4,
∴反比例函数解析式为y=
 .
.把A(2,2)代入y=k1x中,
∴2=2k1,
∴k1=1,
∴正比例函数的解析式为y=x;
(2)把x=-2代入y=x,得y=-2,
∴n=-2;
(3)根据(2)得D(-2,-2),
∵c(2,0),
∴S△ODC=
 ×2×2=2.
×2×2=2.分析:(1)根据正方形的面积为4,易求A点坐标,分别代入函数表达式求解;
(2)把x=-2代入任一解析式可求纵坐标n;
(3)由D点坐标即可求△ODC的面积.
点评:此题要求学生熟练掌握利用待定系数法求函数解析式,同时会利用反比例函数图象和性质解决问题,解题时注意点的坐标与线段长度的联系.

练习册系列答案
相关题目
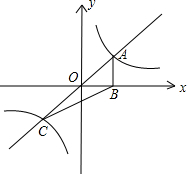 如图,正比例函数y=kx(k>0)与反比例函数y=
如图,正比例函数y=kx(k>0)与反比例函数y=| 1 |
| x |
| A、S=1 | B、S=2 |
| C、S=3 | D、S的值不能确定 |
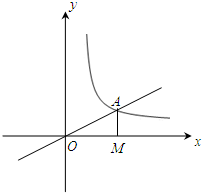 如图,正比例函数
如图,正比例函数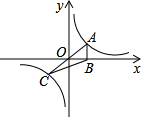 如图,正比例函数y=kx(k>0)与反比例函数y=
如图,正比例函数y=kx(k>0)与反比例函数y= 作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点.
作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点. 已知:如图,正比例函数y=k1x的图象与反比例函数
已知:如图,正比例函数y=k1x的图象与反比例函数