题目内容
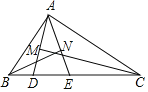
【题目】如图,△ABC的周长为17,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为点N,∠ACB的平分线垂直于AD,垂足为点M,若BC=6,则MN的长度为_____.
【答案】2.5.
【解析】
证明△BNA≌△BNE,得到BA=BE,即△BAE是等腰三角形,同理△CAD是等腰三角形,根据题意求出DE,根据三角形中位线定理计算即可.
解:∵BN平分∠ABC,BN⊥AE,
∴∠NBA=∠NBE,∠BNA=∠BNE,
在△BNA和△BNE中,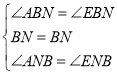
∴△BNA≌△BNE(ASA),
∴BA=BE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴根据等腰三角形三线合一的性质,可得:点N是AE中点,点M是AD中点,
∴MN是△ADE的中位线,
∵BE+CD=AB+AC=17﹣BC=17﹣6=11,
∴DE=BE+CD﹣BC=5,
∴MN=![]() DE=2.5.
DE=2.5.
故答案为:2.5.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目