题目内容
【题目】.如图1,在平面直角坐标系xoy中,M是x轴正半轴上一点,⊙M与x轴的正半轴交于A,B两点,A在B的左侧,且OA,OB的长是方程x2-12x+27=0的两根,ON是⊙M的切线,N为切点,N在第四象限.
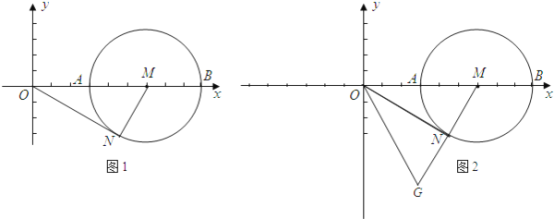
(1)求⊙M的直径的长.
(2)如图2,将△ONM沿ON翻转180°至△ONG,求证△OMG是等边三角形.
(3)求直线ON的解析式.
【答案】(1)6(2)见解析(3)y=![]() x
x
【解析】
试题(1)解方程x2-12x+27=0求出OA=3,OB=9,利用AB=OB-OA计算即可;(2)根据条件证明OM=OG=MN=6即可;(3)过N作NC⊥OM,垂足为C,连结MN,然后利用等边三角形的性质和勾股定理求出OC、CN的长,得到点N的坐标,然后用待定系数法求解析式即可.
试题解析:(1)解方程x2-12x+27="0" 解得:x1=9,x2=3,
∵A在B的左侧,∴OA=3,OB=9,∴AB=OB-OA=6,
∴OM的直径为6
(2))由已知得:MN=GN=3,OG=OM=6,
∴OM=OG=MN=6,∴△OMG是等边三角形.
(3)如图2,过N作NC⊥OM,垂足为C,连结MN,
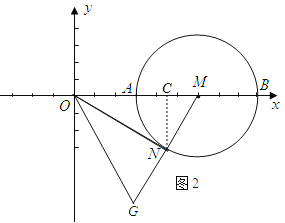
则MN⊥ON,∵△OMG是等边三角形.∴∠CMN=60°,
∠CNM=30° ∴CM=![]() MN=
MN=![]() ,
,
在Rt△CMN中,CN=![]() =
=![]()
∴OC=OM-CM=6-![]() =
=![]()
∴N的坐标(![]() ,-
,-![]() )
)
设直线ON的解析式为y=kx,![]() k=-
k=-![]() ,则k=
,则k=![]()
所以直线ON的解析式为y=![]() x
x

 名校课堂系列答案
名校课堂系列答案【题目】在学校举办的“弘扬社会主义核心价值观”为主题的演讲比赛中,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.