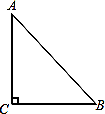题目内容
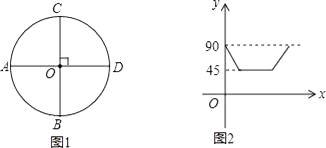
【题目】已知平面内一点P，若点P到两条相交直线l1和l2的距离都相等，且距离均为h（h>0），则称点P叫做直线l1和l2的“h距离点”. 例如图1所示，直线l1和l2互相垂直，交于O点，平面内一点P到两直线的距离都是2，则称点P叫做直线l1和l2的“2距离点”.
（1）若直线l1和l2互相垂直，且交于O点，平面内一点P是直线l1和l2的“7距离点”，直接写出OP的长度为 ；
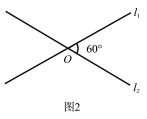
（2）如图2所示，直线l1和l2相交于点O，夹角为60°，已知平面内一点P是直线l1和l2的“3距离点”，求出OP的长度；
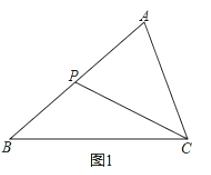
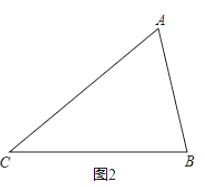
（3）已知三条直线两两相交后形成一个等边三角形，如图3所示，在等边△ABC中，点P是三角形内部一点，且点P分别是等边△ABC三边所在直线的“
距离点”，请你直接写出△ABC的面积是 .
【答案】（1）
（2）6或
（3）
【解析】
（1）根据勾股定理求解即可；
（2）分点P在锐角内部和P在钝角内部两种情况求解即可；
（3）由题意知，点P是三个角平分线的交点，根据等边三角形的性质和勾股定理求出三角形的边长，即可求出三角形的面积.
(1) ；
（2）当点P在锐角内部时，
，
∵
，
∴
，
∴
，
∵
，
∴
，
；
当点P在钝角内部时.
，
∴，
∴
，
∴
，
∴
，
，
，
∴ 
（负值舍去）
∴ 
综上所述，OP的长为6或
（3）
练习册系列答案
相关题目
